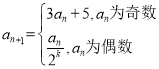题目内容
【题目】如图所示,已知椭圆:![]() (
(![]() )的离心率为
)的离心率为![]() ,右准线方程是直线l:
,右准线方程是直线l:![]() ,点P为直线l上的一个动点,过点P作椭圆的两条切线
,点P为直线l上的一个动点,过点P作椭圆的两条切线![]()
![]() ,切点分别为AB(点A在x轴上方,点B在x轴下方).
,切点分别为AB(点A在x轴上方,点B在x轴下方).
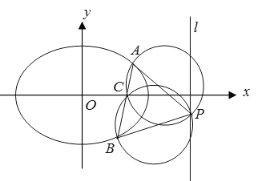
(1)求椭圆的标准方程;
(2)①求证:分别以![]()
![]() 为直径的两圆都恒过定点C;
为直径的两圆都恒过定点C;
②若![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(1)![]() .(2)①答案见解析:②
.(2)①答案见解析:②![]()
【解析】
(1)计算得到![]() ,
,![]() 得到答案.
得到答案.
(2)计算切线![]() :
:![]() ,得到
,得到![]() 坐标,得到
坐标,得到![]() 为直径的圆的圆方程,取
为直径的圆的圆方程,取![]() 计算得到答案;设
计算得到答案;设![]() ,
,![]() ,
,![]() ,解得
,解得![]() 坐标,得到直线方程.
坐标,得到直线方程.
(1)![]() ,准线
,准线![]() ,解得
,解得![]() ,
,![]() ,故
,故![]() ,
,
故椭圆方程为:![]() .
.
(2)①设切点![]() ,当
,当![]() 时,
时,![]() ,
,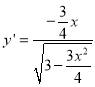 ,
,
故![]() ,则切线
,则切线![]() :
:![]() ,所以点
,所以点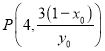 ,
,
以![]() 为直径的圆:
为直径的圆: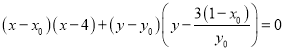 ,
,
由对称性可知定点在x轴上,令![]() 得
得![]() ,过定点
,过定点![]() ,
,
同理,以![]() 为直径的圆过定点
为直径的圆过定点![]() ,得证.
,得证.
②设![]() ,
,![]() ,
,![]() ,因为
,因为![]() ,所以
,所以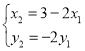 ,
,
又因为 ,所以
,所以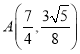 ,
,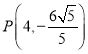 ,
,
所以直线![]() 的方程为
的方程为![]() .
.

 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案【题目】设函数![]() ,
,![]() 为f(x)的导函数.
为f(x)的导函数.
(1)若a=b=c,f(4)=8,求a的值;
(2)若a≠b,b=c,且f(x)和![]() 的零点均在集合
的零点均在集合![]() 中,求f(x)的极小值;
中,求f(x)的极小值;
(3)若![]() ,且f(x)的极大值为M,求证:M≤
,且f(x)的极大值为M,求证:M≤![]() .
.
【题目】交通部门调查在高速公路上的平均车速情况,随机抽查了60名家庭轿车驾驶员,统计其中有40名男性驾驶员,其中平均车速超过![]() 的有30人,不超过
的有30人,不超过![]() 的有10人;在其余20名女性驾驶员中,平均车速超过
的有10人;在其余20名女性驾驶员中,平均车速超过![]() 的有5人,不超过
的有5人,不超过![]() 的有15人.
的有15人.
(1)完成下面的![]() 列联表,并据此判断是否有
列联表,并据此判断是否有![]() 的把握认为,家庭轿车平均车速超过
的把握认为,家庭轿车平均车速超过![]() 与驾驶员的性别有关;
与驾驶员的性别有关;
平均车速超过 | 平均车速不超过 | 合计 | |
男性驾驶员 | |||
女性驾驶员 | |||
合计 |
(2)根据这些样本数据来估计总体,随机调查3辆家庭轿车,记这3辆车中,驾驶员为女性且平均车速不超过![]() 的人数为
的人数为![]() ,假定抽取的结果相互独立,求
,假定抽取的结果相互独立,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考公式: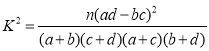
![]()
临界值表:
| 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |