题目内容
5.抛物线x2=2py(p>0)的焦点为F,其准线与双曲线$\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{3}$=1相交于A,B两点,若△ABF为等边三角形,则p的值为( )| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
分析 求出抛物线的焦点坐标,准线方程,然后求出抛物线的准线与双曲线的交点坐标,利用三角形是等边三角形得到p的方程,求出p即可.
解答 解:抛物线的焦点坐标为(0,$\frac{p}{2}$),
准线方程为:y=-$\frac{p}{2}$,
准线方程与双曲线联立可得:$\frac{{x}^{2}}{3}$-$\frac{{p}^{2}}{12}$=1,
解得x=±$\sqrt{3+\frac{{p}^{2}}{4}}$,
因为△ABF为等边三角形,
所以$\frac{\sqrt{3}}{2}$|AB|=p,
即有$\frac{\sqrt{3}}{2}$•2$\sqrt{3+\frac{{p}^{2}}{4}}$=p,
解得p=6.
故选:C.
点评 本题考查抛物线的简单性质,双曲线方程的应用,考查分析问题解决问题的能力以及计算能力,属于中档题.

练习册系列答案
相关题目
13.已知数列{an}满足an+1=an-an-1(n≥2),a1=2017,a2=2016,Sn为数列{an}的前n项和,则S2017的值为( )
| A. | 2017×2016 | B. | 2016 | C. | 2017 | D. | 1 |
20.“α=$\frac{π}{3}$“是“cosα=$\frac{1}{2}$“成立的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
17.2017年“一带一路”国际合作高峰论坛于今年5月14日至15日在北京举行.为高标准完成高峰论坛会议期间的志愿服务工作,将从27所北京高校招募大学生志愿者,某调查机构从是否有意愿做志愿者在某高校访问了80人,经过统计,得到如下丢失数据的列联表:(a,b,d,A,B,表示丢失的数据)
(Ⅰ)求出a,b,d,A,B的值,并判断:能否有99.9%的把握认为有意愿做志愿者与性别有关;
(Ⅱ)若表中无意愿做志愿者的5个女同学中,3个是大学三年级同学,2个是大学四年级同学.现从这5个同学中随机选2同学进行进一步调查,求这2个同学是同年级的概率.
附参考公式及数据:${K^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$,其中n=a+b+c+d.
| 无意愿 | 有意愿 | 总计 | |
| 男 | a | b | 40 |
| 女 | 5 | d | A |
| 总计 | 25 | B | 80 |
(Ⅱ)若表中无意愿做志愿者的5个女同学中,3个是大学三年级同学,2个是大学四年级同学.现从这5个同学中随机选2同学进行进一步调查,求这2个同学是同年级的概率.
附参考公式及数据:${K^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$,其中n=a+b+c+d.
| P(K2≥k0) | 0.40 | 0.25 | 0.10 | 0.010 | 0.005 | 0.001 |
| k0 | 0.708 | 1.323 | 2.706 | 6.635 | 7.879 | 10.828 |
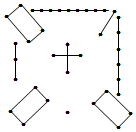 洛书古称龟书,是阴阳五行术数之源,在古代传说中有神龟出于洛水,其甲壳上有如图所示图案,结构是戴九履一,左三右七,二四为肩,六八为足,以五居中,洛书中蕴含的规律奥妙无穷,比如:42+92+22=82+12+62.据此你能得到类似等式是42+32+82=22+72+62.
洛书古称龟书,是阴阳五行术数之源,在古代传说中有神龟出于洛水,其甲壳上有如图所示图案,结构是戴九履一,左三右七,二四为肩,六八为足,以五居中,洛书中蕴含的规律奥妙无穷,比如:42+92+22=82+12+62.据此你能得到类似等式是42+32+82=22+72+62.