Question

在一次抽奖活动中，有甲、乙等6人获得抽奖的机会。抽奖规则如下：主办方先从6人中随机抽取两人均获奖1000元，再从余下的4人中随机抽取1人获奖600元，最后还从这4人中随机抽取1人获奖400元。

（Ⅰ）求甲和乙都不获奖的概率；

（Ⅱ）设X是甲获奖的金额，求X的分布列和均值。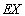

Answer 1

解：（Ⅰ）设“甲和乙都不获奖”为事件A ,   分

则P（A）=， 

答：甲和乙都不获奖的概率为. 

（Ⅱ）X的所有可能的取值为0，400，600，1000，

P(X=0)=, P(X=400)= , P(X=600)= ,

P(X=1000)= ,

∴X的分布列为

X	0	400	600	1000
P

                                                       

∴E(X)=0×+400×+600×+1000×=500(元). 

答: 甲获奖的金额的均值为500(元).