题目内容
20．
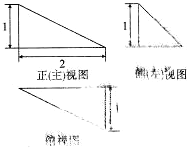某三棱锥的三视图如图所示，其中三个视图都是直角三角形，则该三棱锥的体积为（ ）| A． | $\frac{1}{3}$ | B． | $\frac{2}{3}$ | C． | 1 | D． | 6 |
分析 由已知中的三视图可得：该几何体是一个以俯视图为底面的三棱锥，代入棱锥体积公式，可得答案．
解答 解：由已知中的三视图可得：该几何体是一个以俯视图为底面的三棱锥，
底面面积S=$\frac{1}{2}$×2×1=1，
高h=1，
故体积V=$\frac{1}{3}Sh$=$\frac{1}{3}$，
故选：A
点评 本题考查的知识点是棱锥的体积和表面积，简单几何体的三视图，难度中档．
练习册系列答案
相关题目
10．若函数$f（x）=\left\{{\begin{array}{l}{\frac{{3（1-{2^x}）}}{{{2^x}+1}}，（-1≤x≤1）}\\{-\frac{1}{4}（{x^3}+3x），（x＜-1或x＞1）}\end{array}}\right.$对任意的m∈[-3，2]，总有f（mx-1）+f（x）＞0恒成立，则x的取值范围是（ ）
| A． | $（{-\frac{1}{2}，\frac{1}{3}}）$ | B． | （-1，2） | C． | $（{-\frac{4}{3}，-\frac{1}{2}}）$ | D． | （-2，3） |
11．设随机变量ξ服从正态分布N（μ，7），若P（ξ＜2）=P（ξ＞4），则μ 与Dξ的值分别为（ ）
| A． | $μ=\sqrt{3}，Dξ=\sqrt{7}$ | B． | $μ=\sqrt{3}，Dξ=7$ | C． | μ=3，Dξ=7 | D． | $μ=3，Dξ=\sqrt{7}$ |
12．已知集合A={x|1＜x＜3}，B={x|x＞2}，则A∪∁RB=（ ）
| A． | {x|x≤2} | B． | {x|2＜x＜3} | C． | {x|x＜3} | D． | {x|1＜x≤2} |
如图，在三棱柱ABC-A1B1C1中，AA1⊥底面ABC，且△ABC为等边三角形，AA1=AB=6，D为AC的中点．
10．已知 a＞0，b＞0，双曲线 C1：$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1，圆C2：x 2+y 2-2ax+$\frac{3}{4}$a2=0，若双曲线C1的渐近线与圆C2相切，则双曲线 C1 的离心率是（ ）
| A． | $\frac{{2\sqrt{3}}}{3}$ | B． | $\sqrt{2}$ | C． | 2 | D． | $\sqrt{5}$ |