题目内容
5.实数x、y满足约束条件$\left\{\begin{array}{l}x-y-2≤0\\ x+2y-5≥0\\ y-2≤0\end{array}\right.则z=\frac{y}{x+1}$的取值范围为[$\frac{1}{4},1$].分析 由约束条件作出可行域,再由$z=\frac{y}{x+1}$的几何意义,即可行域内的动点与定点P(-1,0)连线的斜率得答案.
解答 解:由约束条件作出可行域如图,
联立$\left\{\begin{array}{l}{x-y-2=0}\\{x+2y-5=0}\end{array}\right.$,解得A(3,1),
联立$\left\{\begin{array}{l}{y=2}\\{x+2y-5=0}\end{array}\right.$,解得B(1,2).
$z=\frac{y}{x+1}$的几何意义为可行域内的动点与定点P(-1,0)连线的斜率.
∵${k}_{PA}=\frac{1}{4},{k}_{PB}=1$,
∴$z=\frac{y}{x+1}$的取值范围为[$\frac{1}{4},1$].
故答案为:[$\frac{1}{4},1$].
点评 本题考查简单的线性规划,考查数形结合的解题思想方法和数学转化思想方法,是中档题.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
16.已知函数$f(x)=\left\{{\begin{array}{l}{{e^x},x≥-1}\\{ln(-x),x<-1}\end{array}}\right.$,则“x=0”是“f(x)=1”的( )
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
20.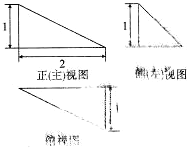 某三棱锥的三视图如图所示,其中三个视图都是直角三角形,则该三棱锥的体积为( )
某三棱锥的三视图如图所示,其中三个视图都是直角三角形,则该三棱锥的体积为( )
 某三棱锥的三视图如图所示,其中三个视图都是直角三角形,则该三棱锥的体积为( )
某三棱锥的三视图如图所示,其中三个视图都是直角三角形,则该三棱锥的体积为( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | 1 | D. | 6 |
17.正方体的内切球和外接球的表面积之比为( )
| A. | 1:2 | B. | 1:3 | C. | 1:4 | D. | 2:3 |
14.平面内有两定点A,B及动点P,设命题甲:“|PA|与|PB|之差的绝对值是定值”,命题乙:“点P的轨迹是以A,B为焦点的双曲线”,那么命题甲是命题乙的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |