Question

已知F₁、F₂分别是双曲线

x2

a2

-

y2

b2

=1(a＞0，b＞0)的左右焦点，A为双曲线的右顶点，线段AF₂的垂直平分线交双曲线与P，且|PF₁|=3|PF₂|，则该双曲线的离心率是（　　）

• A、

  3

• B、

  2

• C、

  -1+ 17

  2

• D、

  1+ 17

  2

Answer 1

考点：双曲线的标准方程

专题：圆锥曲线的定义、性质与方程

分析：由题设条件，分别求出|PF₁|，|PF₂|，|BF₁|，|BF₂|的长，再由勾股定理进行求解．

解答： 解：∵F₁、F₂分别是双曲线

x2

a2

-

y2

b2

=1(a＞0，b＞0)的左右焦点，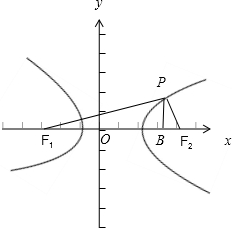
A为双曲线的右顶点，且|PF₁|=3|PF₂|，
∴|PF₁|-|PF₂|=2|PF₂|=2a，
∴|PF₁|=3a，|PF₂|=a，
∵线段AF₂的垂直平分线交双曲线于P，
∴P点横坐标x_P=

1

2

(a+c)，
设线段AF₂的垂直平分线交x轴于B，则|F₁B|=

1

2

a+

3

2

c，|BF₂|=

c-a

2

，
∴（3a）²-（

1

2

a+

3

2

c）²=a²-（

c-a

2

）²，
整理，得当8a²-2c²-2ac=0，
∴e²+e-4=0，
解得e=

-1+ 17

2

，或e=

-1- 17

2

（舍）．
故选：C．

点评：本题考查双曲线的离心率的求法，是中档题，解题时要熟练掌握双曲线的简单性质，注意勾股定理的合理运用．