题目内容
7．已知i是虚数单位，则复数$\frac{5+3i}{4-i}$的共轭复数是（ ）| A． | 1-i | B． | -1+i | C． | 1+i | D． | -1-i |
分析 利用复数代数形式的乘除运算化简得答案．
解答 解：$\frac{5+3i}{4-i}=\frac{{（{5+3i}）（{4+i}）}}{{（{4-i}）（{4+i}）}}=\frac{{20+17i+3{i^2}}}{{{4^2}-{i^2}}}=\frac{17+17i}{17}=1+i$，
∴复数$\frac{5+3i}{4-i}$的共轭复数是1-i．
故选：A．
点评 本题考查复数代数形式的乘除运算，考查了共轭复数的概念，是基础题．
练习册系列答案
名校课堂系列答案
相关题目
17．执行如图所示的程序框图，则输出的s=（ ）
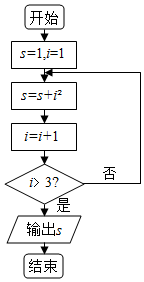
| A． | 6 | B． | 15 | C． | 25 | D． | 3 |
12．已知函数f（x）=2sin（2x+φ）（|φ|＜$\frac{π}{2}}$）图象过点（0，$\sqrt{3}}$），则f（x）图象的一个对称中心是（ ）
| A． | $（-\frac{π}{3}，0）$ | B． | $（-\frac{π}{6}，0）$ | C． | $（\frac{π}{6}，0）$ | D． | $（\frac{π}{12}，0）$ |
19．
已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的图象（部分）如图所示，把f（x）的图象上各点向左平移$\frac{1}{2}$单位，得到函数g（x）的图象，则g（$\frac{5}{2}$）=（ ）
已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的图象（部分）如图所示，把f（x）的图象上各点向左平移$\frac{1}{2}$单位，得到函数g（x）的图象，则g（$\frac{5}{2}$）=（ ）| A． | -1 | B． | 1 | C． | -$\sqrt{3}$ | D． | $\sqrt{3}$ |