题目内容
16.求数列$\frac{1}{1+\sqrt{3}}$,$\frac{1}{\sqrt{2}+2}$,…,$\frac{1}{\sqrt{n}+\sqrt{n+2}}$,…的前n项和Sn.分析 通过分母有理化、裂项可知$\frac{1}{\sqrt{n}+\sqrt{n+2}}$=$\frac{1}{2}$($\sqrt{n+2}$-$\sqrt{n}$),进而并项相加即得结论.
解答 解:∵$\frac{1}{\sqrt{n}+\sqrt{n+2}}$=$\frac{\sqrt{n+2}-\sqrt{n}}{(\sqrt{n}+\sqrt{n+2})(\sqrt{n+2}-\sqrt{n})}$=$\frac{1}{2}$($\sqrt{n+2}$-$\sqrt{n}$),
∴Sn=$\frac{1}{2}$($\sqrt{3}$-1+$\sqrt{4}$-$\sqrt{2}$+…+$\sqrt{n+2}$-$\sqrt{n}$)
=$\frac{1}{2}$(-1-$\sqrt{2}$+$\sqrt{n+1}$+$\sqrt{n+2}$).
点评 本题考查数列的求和,考查裂项相消法,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
6.已知l,m,n是不同的直线,α,β,γ是不重合的平面,下列命题中正确的个数为( )
①若m⊥α,m⊥β,则α∥β;②若α⊥γ,β⊥γ,则α∥β
③若m∥α,m∥β,则α∥β;④l∥α,m?α,则l∥m.
①若m⊥α,m⊥β,则α∥β;②若α⊥γ,β⊥γ,则α∥β
③若m∥α,m∥β,则α∥β;④l∥α,m?α,则l∥m.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
7.已知i是虚数单位,则复数$\frac{5+3i}{4-i}$的共轭复数是( )
| A. | 1-i | B. | -1+i | C. | 1+i | D. | -1-i |
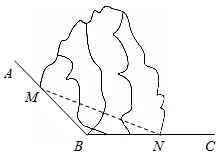 如图所示,AB,BC是两条傍山公路,∠ABC=120°,现在拟从M,N两处修建一条隧道(单位:千米).
如图所示,AB,BC是两条傍山公路,∠ABC=120°,现在拟从M,N两处修建一条隧道(单位:千米).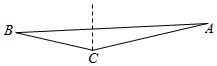 如图,一艘船现在灯塔C北偏东75°的点A且AC=3海里,当船航行了$\sqrt{21}$海里后到达点B,若点B在灯塔C西偏北15°方向上,则B,C两点的距离为$\sqrt{3}$海里.
如图,一艘船现在灯塔C北偏东75°的点A且AC=3海里,当船航行了$\sqrt{21}$海里后到达点B,若点B在灯塔C西偏北15°方向上,则B,C两点的距离为$\sqrt{3}$海里.