题目内容
设变量x，y满足2xy=1（x＜0），则x+2y的最大值为 ．
考点：基本不等式
专题：不等式的解法及应用
分析：变形利用基本不等式的性质即可得出．
解答：
解：∵变量x，y满足2xy=1（x＜0），∴2y=
＜0．
∴x+2y=x+
=-（-x+
）≤-2
=-2，当且仅当x=-1时去等号．
∴x+2y的最大值为-2．
故答案为：-2．
| 1 |
| x |
∴x+2y=x+
| 1 |
| x |
| 1 |
| -x |
-x•
|
∴x+2y的最大值为-2．
故答案为：-2．
点评：本题考查了基本不等式的性质，属于基础题．
练习册系列答案
中考利剑中考试卷汇编系列答案
教育世家状元卷系列答案
黄冈课堂作业本系列答案
单元加期末复习先锋大考卷系列答案
相关题目
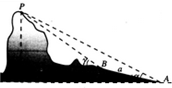如图：在山脚A测得山顶P的仰角为α=30°，沿倾斜角β=15°的斜坡向上走100米到B，在B处测得山顶P的仰角为γ=60°，则山高h=