题目内容
若函数f(x)=
-a与x轴有两个不同的交点,则实数a的取值范围为 .
| x |
| ex |
考点:函数的图象
专题:计算题,作图题,导数的综合应用
分析:令g(x)=
,求导g′(x)=
,从而确定函数的单调性及最值,结合函数的图象求实数a的取值范围.
| x |
| ex |
| 1-x |
| ex |
解答:
解:令g(x)=
,g′(x)=
,
故g(x)在(-∞,1]上单调递增,在[1,+∞)h上单调递减,
故g(x)≤g(1)=
;
作函数g(x)=
的图象如下,

故0<a<
,
故答案为:(0,
).
| x |
| ex |
| 1-x |
| ex |
故g(x)在(-∞,1]上单调递增,在[1,+∞)h上单调递减,
故g(x)≤g(1)=
| 1 |
| e |
作函数g(x)=
| x |
| ex |

故0<a<
| 1 |
| e |
故答案为:(0,
| 1 |
| e |
点评:本题考查了导数的综合应用及函数的图象的作法与应用,属于中档题.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
以茎叶图记录了甲乙两组各五名学生在一次英语听力测试中的成绩(单位:分),已知甲组数据的中位数为15,乙组数据的平均数为16.8,则x,y的值分别为( )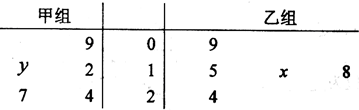

| A、5,2 | B、5,5 |
| C、8,5 | D、8,8 |
按如图所示的程序框图,在运行后输出的结果为( )


| A、7 | B、8 | C、9 | D、10 |
若|
|=2,|
|=1,
和
夹角为60°,则|
+2
|=( )
| a |
| b |
| a |
| b |
| a |
| b |
| A、2 | ||
| B、4 | ||
| C、3 | ||
D、2
|
 如图,设A为半径为1圆周上一定点,在圆周上等可能的任取一点B,则弦长|AB|超过
如图,设A为半径为1圆周上一定点,在圆周上等可能的任取一点B,则弦长|AB|超过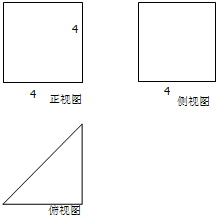 一个几何体的三视图如图所示,则这个几何体的表面积等于
一个几何体的三视图如图所示,则这个几何体的表面积等于