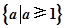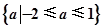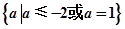题目内容
已知命题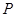 :函数
:函数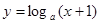 在
在 内单调递减;
内单调递减;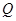 :曲线
:曲线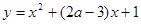 与
与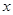 轴没有交点.如果“
轴没有交点.如果“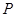 或
或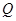 ”是真命题,“
”是真命题,“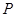 且
且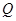 ”是假命题,则实数
”是假命题,则实数 的取值范围是( )
的取值范围是( )
A.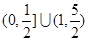 | B.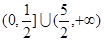 | C.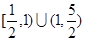 | D.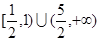 |
A
解析试题分析:根据对数函数的单调性与底数的关系,我们可以判断出命题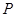 为真时,实数
为真时,实数 的取值范围,根据二次不等式恒成立的充要条件,可以判断出命题
的取值范围,根据二次不等式恒成立的充要条件,可以判断出命题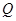 为真时,实数
为真时,实数 的取值范围,进而根据“
的取值范围,进而根据“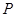 或
或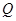 ”是真命题,“
”是真命题,“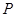 且
且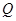 ”是假命题,得到命题
”是假命题,得到命题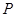 和
和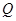 必然一真一假,分别讨论
必然一真一假,分别讨论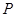 真
真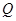 假时,和
假时,和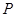 假
假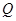 真时,实数
真时,实数 的取值范围,综合讨论结果,即可得到答案.
的取值范围,综合讨论结果,即可得到答案.
考点:命题的真假判断与应用;对数函数的单调性与特殊点;一元二次不等式的应用.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
已知函数 则
则 是
是 成立的 ( )
成立的 ( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
已知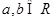 ,则
,则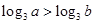 是
是  的( )
的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
命题“若a>b,则2a>2b-1”的否命题为( )
| A.若a>b,则有2a≤2b-1. | B.若a≤b,则有2a≤2b-1. |
| C.若a≤b,则有2a>2b-1. | D.若2a≤2b-1,则有a≤b. |
原命题为“若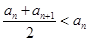 ,
,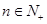 ,则
,则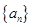 为递减数列”,关于逆命题,否命题,逆否命题真假性的判断依次如下,正确的是( )
为递减数列”,关于逆命题,否命题,逆否命题真假性的判断依次如下,正确的是( )
| A.真,真,真 | B.假,假,真 | C.真,真,假 | D.假,假,假 |
用反证法证明某命题时,对结论:“自然数 中恰有一个偶数”正确的反设为( )
中恰有一个偶数”正确的反设为( )
A. 都是奇数 都是奇数 |
B. 都是偶数 都是偶数 |
C. 中至少有两个偶数 中至少有两个偶数 |
D. 中至少有两个偶数或都是奇数 中至少有两个偶数或都是奇数 |
设命题 ,则
,则 为( )
为( )
A. | B. |
C. | D. |
[2014·黄山模拟]“-3<m<5”是“方程 +
+ =1表示椭圆”的( )
=1表示椭圆”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
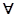 x∈[1,2],x2-a≥0”,命题q:“
x∈[1,2],x2-a≥0”,命题q:“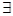 x∈R使x2+2ax+2-a=0”,若命题“p且q”是真命题,则实数a的取值范围是( )
x∈R使x2+2ax+2-a=0”,若命题“p且q”是真命题,则实数a的取值范围是( )