题目内容

函数f(x)=
x2+5
x2+4
的最小值为（　　）
A．2B．
5
2
C．1D．不存在
由于 f(x)=
x2+5
x2+4
=
(
x2+4
)2+1
x2+4
=
x2+4
+
1
x2+4

令t=
x2+4
，则t≥2，f（t）=t+
1
t
在（2，+∞）上单调递增，
∴f(x)=
x2+5
x2+4
的最小值为：
5
2

故选B．
练习册系列答案
相关题目
(12分)已知：函数，                                                           
　　(1)求：函数f(x)的定义域；
　　(2)判断函数f(x)的奇偶性并说明理由；
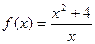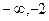　　(3)判断函数f(x)在()上的单调性，并用定义加以证明。
（文）设x∈R，[x]表示不大于x的最大整数，如：[π]=3，[-1.2]=-2，[0.5]=0，则使[x2-1]=3的x的取值范围是（　　）
A．[2，
5
）		B．（-
5
，-2]		C．（-
5
，-2]∪[2，
5
）		D．[-
5
，-2]∪[2，
5
]
已知函数f(x)=x2+x+
m
x
在[1，+∞）上是增函数，则实数m的取值范围是（　　）
A．m≤3B．m≤-3C．m≥3D．m≥-3
给出命题：若a，b是正常数，且a≠b，x，y∈（0，+∞），则
a2
x
+
b2
y
≥
(a+b)2
x+y
（当且仅当
a
x
=
b
y
时等号成立）．根据上面命题，可以得到函数f(x)=
2
x
+
9
1-2x
（x∈(0，
1
2
)）的最小值及取最小值时的x值分别为（　　）
A．11+6
2
，
2
13
B．11+6
2
，
1
5
C．5，
2
13
D．25，
1
5
已知函数f（x）=
cx+1，(1＜x＜c)
2-
x
c2
+1，(x≥c)
满足f(c3)=
9
8
．
（1）求常数c的值；
（2）解关于x的不等式f(x)＜4
2
+1．
已知某商品生产成本C与产量q的函数关系式为C=100+4q，价格p与产量q的函数关系式为p=25-
1
8
q．求产量q等于______，利润L最大．
已知g（x）=1-x，f[g（x）]=2-x2，
（1）求f（x）的解析式；
（2）h（x）=
f(x)-1
x2
-a，若h（x）在x∈[-3，-1]上的最大值是-
5
3
，求a的值．
已知f（x）是定义在R上的偶函数，对任意的x∈R都有f（x+6）=f（x）+2f（3），f（-1）=2，则f（2011）=（　　）
A．1B．2C．3D．4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网