Question

如图，四棱锥P-ABCD的底面是正方形，侧面PAB⊥平面ABCD，AP=AB=1，∠PAB=

2π

3

，点M，N，E分别在线段PD，AC，BC上，且满足DM=CN，EN∥AB．
（Ⅰ）求证：平面EMN∥平面PAB；
（Ⅱ）设

DM

DP

=λ，若二面角A-MN-E的大小为

2π

3

，求λ的值．

Answer 1

考点：与二面角有关的立体几何综合题,平面与平面平行的判定

专题：空间位置关系与距离,空间角

分析：（Ⅰ）由侧面PAB⊥平面ABCD，AD⊥AB，得AD⊥平面PAB，从而AD⊥PA，又PA=AB=1，进而PD=AC=

2

，DM=CN，过M作MR∥AD，交AP于R，过N作NQ∥AD交AB于Q，RMNQ为平行四边形，由此能证明平面EMN∥平面PAB．
（Ⅱ）以B为原点，建立空间直角坐标系，利用向量法能求出λ=

2( 6 -1)

5

．

解答： （Ⅰ）证明：∵侧面PAB⊥平面ABCD，侧面PAB∩平面ABCD=AB，
由ABCD为正方形，得AD⊥AB，AD?平面ABCD，
∴AD⊥平面PAB，又PA?平面PAB，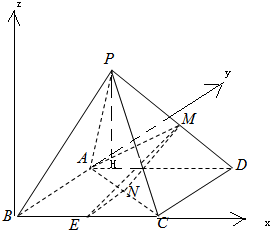
∴AD⊥PA，又PA=AB=1，
∴PD=AC=

2

，DM=CN，
过M作MR∥AD，交AP于R，过N作NQ∥AD交AB于Q，
∴RM

∥

.

QN，∴RMNQ为平行四边形，
∴MN∥RQ，又RQ?平面PAB，MN不包含于平面PAB，
∴MN∥平面PAB，
又EN∥AD，AD?平面PAB，∴EN∥平面PAB，
∵MN，EN?平面EMN，
∴平面EMN∥平面PAB．
（Ⅱ）以B为原点，建立如图所示的空间直角坐标系，
B（0，0，0），C（1，0，0），D（1，1，0），
H（0，

3

2

，0），H为P在平面ABCD内的射影，
P（0，

3

2

，

3

2

），令

DM

=λ

DP

，0≤λ≤1，
则

CM

=λ

CA

，

CE

=λ

CB

，
∵平面MNE∥平面PAB，AD⊥平面PAB，
∴

α

=(1，0，0)为平面法向量，
设

p

=（x，y，z）为平面AMN的法向量，

AM

=(1-λ，

1

2

λ，

3

2

λ)，

AN

=（1-λ，-1+λ，0），

p • AM =(1-λ)x+ 1 2 λy+ 3 2 λz=0 p • AN =(1-λ)x+(λ-1)y=0

，
取x=1，得

p

=（1，1，

λ-2

3 λ

），
∵二面角A-MN-E的大小为

2π

3

，
∴|cos＜

α

，

p

＞|=

1

1+1+( λ-2 3 λ )2

=|cos

2π

3

|=

1

2

，
∴（

λ-2

3 λ

）²=2，∵λ∈[0，1]，∴-

λ-2

3 λ

=

2

，
解得λ=

2( 6 -1)

5

．

点评：本题考查平面与平面平行的证明，考查λ的值的求法，解题时要认真审题，注意向量法的合理运用．