题目内容
11.在△ABC中,已知sin(A+B)=2sinAcosB,那么△ABC一定是( )| A. | 等腰直角三角形 | B. | 直角三角形 | C. | 等腰三角形 | D. | 等边三角形 |
分析 由正弦定理可得2acosB=c,由余弦定理可得cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$,可得$\frac{c}{2a}$=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$,化简可得a=b,进而可得答案.
解答 解:∵在△ABC中,已知sin(A+B)=2sinAcosB,
∴sinC=2sinAcosB,
由正弦定理可得 2acosB=c,又由余弦定理可得cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$,
∴cosB=$\frac{c}{2a}$=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$,
∴a2=b2,
故a=b,故△ABC一定是等腰三角形,
故选:C.
点评 本题三角形形状的判断,考查正弦定理,余弦定理的应用,得到 cosB=$\frac{c}{2a}$=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$,是解题的关键.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
1.一个几何体的三视图如图所示,其中俯视图为正方形,则该几何体最大的侧面的面积为( )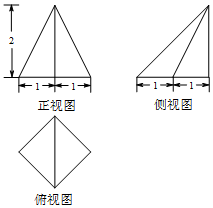

| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
19.在复平面内,复数z=$\frac{2i}{1+i}$(i为虚数单位)的共轭复数对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
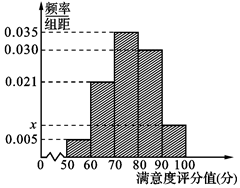 共享单车是指由企业在校园、公交站点、商业区、公共服务区等场所提供的自行车单车共享服务,由于其依托“互联网+”,符合“低碳出行”的理念,已越来越多地引起了人们的关注.某部门为了对该城市共享单车加强监管,随机选取了100人就该城市共享单车的推行情况进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照 分成5组,制成如图所示频率分直方图.
共享单车是指由企业在校园、公交站点、商业区、公共服务区等场所提供的自行车单车共享服务,由于其依托“互联网+”,符合“低碳出行”的理念,已越来越多地引起了人们的关注.某部门为了对该城市共享单车加强监管,随机选取了100人就该城市共享单车的推行情况进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照 分成5组,制成如图所示频率分直方图.