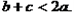题目内容
在任何两边都不相等的锐角△ABC中,2sin2A-cos2A=2.(1)求角B的取值范围.
(2)求函数y=2sin2B+sin(2B+![]() )的值域.
)的值域.
解:(1)∵2sin2A-cos2A=2,∴sin2A=![]() .
.
∴sinA=±![]() .又∵0<A<
.又∵0<A<![]() ,∴sinA=
,∴sinA=![]() .∴A=
.∴A=![]() .
.
又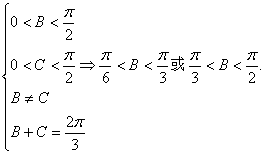
(2)∵y=2sin2B+sin(2B+![]() )=2×
)=2×![]() +
+![]() sin2B+
sin2B+![]() cos2B,
cos2B,
∴y=sin(2B-![]() )+1.
)+1.
由(1)知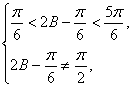 ∴
∴![]() <y<2.
<y<2.
∴函数y=2sin2B+sin(2B+![]() )的值域为(
)的值域为(![]() ,2).
,2).

练习册系列答案
相关题目

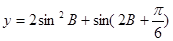 的值域; (3)求证:
的值域; (3)求证:
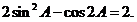
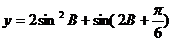 的值域;
的值域;