题目内容
12．设{an}是等差数列，下列结论中正确的是（ ）| A． | 若a1+a2＞0，则a2+a3＞0 | B． | 若a1+a2＜0，则a2+a3＜0 | ||
| C． | 若0＜a1＜a2，则a2＞$\sqrt{{a}_{1}{a}_{3}}$ | D． | 若a1＜0，则（a2-a1）（a2-a3）＜0 |
分析 根据{an}是等差数列，结合等差数列的定义及基本不等式等，逐一分析四个答案的正误，可得答案．
解答 解：若a1+a2＞0，d＜0，则a2+a3＞0不一定成立，故A错误；
若a1+a2＜0，d＞0，则a2+a3＜0不一定成立，故B错误；
若0＜a1＜a2，则a2=$\frac{{a}_{1}+{a}_{3}}{2}$＞$\sqrt{{a}_{1}{a}_{3}}$，故C正确；
若a1＜0，则（a2-a1）（a2-a3）=-d2≤0，故D错误；
故选：C
点评 本题以命题的真假判断与应用为载体，考查了等差数列，基本不等式，难度中档．
练习册系列答案
阅读快车系列答案
相关题目
20．
从某小区随机抽取40个家庭，收集了这40个家庭去年的月均用水量（单位：吨）的数据，整理得到频数分布表和频率分布直方图．
（1）求频率分布直方图中a，b的值；
（2）从该小区随机选取一个家庭，试估计这个家庭去年的月均用水量不低于6吨的概率；
（3）在这40个家庭中，用分层抽样的方法从月均用水量不低于6吨的家庭里抽取一个容量为7的样本，将该样本看成一个总体，从中任意选取2个家庭，求其中恰有一个家庭的月均用水量不低于8吨的概率．
从某小区随机抽取40个家庭，收集了这40个家庭去年的月均用水量（单位：吨）的数据，整理得到频数分布表和频率分布直方图．| 分组 | 频数 |
| [2，4） | 2 |
| [4，6） | 10 |
| [6，8） | 16 |
| [8，10） | 8 |
| [10，12] | 4 |
| 合计 | 40 |
（2）从该小区随机选取一个家庭，试估计这个家庭去年的月均用水量不低于6吨的概率；
（3）在这40个家庭中，用分层抽样的方法从月均用水量不低于6吨的家庭里抽取一个容量为7的样本，将该样本看成一个总体，从中任意选取2个家庭，求其中恰有一个家庭的月均用水量不低于8吨的概率．
7．
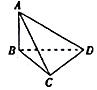要测量底部不能到达的电视塔AB的高度，在C点测得塔顶A的仰角是45°，在D点测得塔顶A的仰角是30°，并测得水平面上的∠BCD=120°，CD=40m，则电视塔的高度为（ ）
要测量底部不能到达的电视塔AB的高度，在C点测得塔顶A的仰角是45°，在D点测得塔顶A的仰角是30°，并测得水平面上的∠BCD=120°，CD=40m，则电视塔的高度为（ ）| A． | 40m | B． | 20m | C． | 305m | D． | （20$\sqrt{6}$-40）m |
