ΧβΡΩΡΎ»ί
“―÷ΣΆ÷‘≤ΒΡ÷––Ρ‘ΎΉχ±ξ‘≠ΒψOΘ§ΫΙΒψ‘ΎX÷α…œΘ§F1Θ§F2Ζ÷±π «Ά÷‘≤ΒΡΉσΓΔ”“ΫΙΒψΘ§M «Ά÷‘≤ΕΧ÷αΒΡ“ΜΗωΕΥΒψΘ§ΓςMF1F2ΒΡΟφΜΐΈΣ4Θ§ΙΐF1ΒΡ÷±œΏl”κΆ÷‘≤ΫΜ”ΎAΘ§BΝΫΒψΘ§ΓςABF2ΒΡ÷ή≥ΛΈΣ8
Θ°
Θ®ΔώΘ©«σ¥ΥΆ÷‘≤ΒΡΖΫ≥ΧΘΜ
Θ®ΔρΘ©»τN «Ήσ±ξΤΫΟφΡΎ“ΜΕ·ΒψΘ§G «ΓςMF1F2ΒΡ÷Ί–ΡΘ§«“
•
=0Θ§«σΕ·ΒψNΒΡΙλΦΘΖΫ≥ΧΘΜ
Θ®ΔσΘ©Βψp…σ¥ΥΆ÷‘≤…œ“ΜΒψΘ§ΒΪΖ«ΕΧ÷αΕΥΒψΘ§≤Δ«“ΙΐPΩ…ΉςΘ®ΔρΘ©÷–Υυ«σΒΟΙλΦΘΒΡΝΫΧθ≤ΜΆ§ΒΡ«–œΏΘ§QΓΔR «ΝΫΗω«–ΒψΘ§«σ
•
ΒΡΉν–Γ÷ΒΘ°
| 2 |
Θ®ΔώΘ©«σ¥ΥΆ÷‘≤ΒΡΖΫ≥ΧΘΜ
Θ®ΔρΘ©»τN «Ήσ±ξΤΫΟφΡΎ“ΜΕ·ΒψΘ§G «ΓςMF1F2ΒΡ÷Ί–ΡΘ§«“
| GF2 |
| ON |
Θ®ΔσΘ©Βψp…σ¥ΥΆ÷‘≤…œ“ΜΒψΘ§ΒΪΖ«ΕΧ÷αΕΥΒψΘ§≤Δ«“ΙΐPΩ…ΉςΘ®ΔρΘ©÷–Υυ«σΒΟΙλΦΘΒΡΝΫΧθ≤ΜΆ§ΒΡ«–œΏΘ§QΓΔR «ΝΫΗω«–ΒψΘ§«σ
| PQ |
| PR |
ΩΦΒψΘΚ÷±œΏ”κ‘≤ΉΕ«ζœΏΒΡΉέΚœΈ Χβ
Ή®ΧβΘΚΦΤΥψΧβ,ΤΫΟφœρΝΩΦΑ”Π”Ο,÷±œΏ”κ‘≤,‘≤ΉΕ«ζœΏΒΡΕ®“εΓΔ–‘÷ ”κΖΫ≥Χ
Ζ÷ΈωΘΚΘ®ΔώΘ©…η≥ωΆ÷‘≤ΖΫ≥ΧΘ§”…Ά÷‘≤ΒΡΕ®“εΩ…ΒΟaΘ§‘Ό”…ΟφΜΐΙΪ ΫΘ§ΫαΚœaΘ§bΘ§cΒΡΙΊœΒΘ§Φ¥Ω…ΒΟΒΫΆ÷‘≤ΖΫ≥ΧΘΜ
Θ®ΔρΘ©…ηNΘ®xΘ§yΘ©Θ§”…÷Ί–ΡΉχ±ξΙΪ ΫΘ§ΫαΚœœρΝΩΒΡ ΐΝΩΜΐΉχ±ξΙΪ ΫΘ§Φ¥Ω…ΒΟΒΫΙλΦΘΖΫ≥ΧΘΜ
Θ®ΔσΘ©≈–ΕœΕ·ΒψNΒΡΙλΦΘΘ§…ηPΘ®mΘ§nΘ©Θ§‘ρΗυΨίΤΫΟφΦΗΚΈ÷Σ ΕΒΟΒΫ|
|=|
|Θ§ΦΑcosΘΦ
Θ§
ΘΨΘ§¥”ΕχΗυΨίΤΫΟφœρΝΩ ΐΝΩΜΐΒΡΕ®“εΦΑΨυ÷Β≤ΜΒ» ΫΒΟ
•
ΒΡΉν–Γ÷ΒΘ°
Θ®ΔρΘ©…ηNΘ®xΘ§yΘ©Θ§”…÷Ί–ΡΉχ±ξΙΪ ΫΘ§ΫαΚœœρΝΩΒΡ ΐΝΩΜΐΉχ±ξΙΪ ΫΘ§Φ¥Ω…ΒΟΒΫΙλΦΘΖΫ≥ΧΘΜ
Θ®ΔσΘ©≈–ΕœΕ·ΒψNΒΡΙλΦΘΘ§…ηPΘ®mΘ§nΘ©Θ§‘ρΗυΨίΤΫΟφΦΗΚΈ÷Σ ΕΒΟΒΫ|
| PQ |
| PR |
| PQ |
| PR |
| PQ |
| PR |
Ϋβ¥πΘΚ
ΫβΘΚΘ®ΔώΘ©”…Χβ“β…ηΆ÷‘≤ΒΡΖΫ≥ΧΈΣ
+
=1(aΘΨbΘΨ0)Θ§
“ρΈΣM «Ά÷‘≤ΕΧ÷αΒΡ“ΜΗωΕΥΒψΘ§ΙΐF1ΒΡ÷±œΏl”κΆ÷‘≤ΫΜ”ΎAΘ§BΝΫΒψΘ§
ΓςMF1F2ΒΡΟφΜΐΈΣ4Θ§ΓςABF2ΒΡ÷ή≥ΛΈΣ8
Θ§
Υυ“‘ 4a=8
Θ§
•b•2c=4Θ§
Γύ
Γύb=c=2Θ§a=2
Θ§
Υυ“‘Θ§Υυ«σΒΡΆ÷‘≤ΖΫ≥ΧΈΣ
+
=1Θ°
Θ®ΔρΘ©…ηNΘ®xΘ§yΘ©Θ§‘ρ”…Θ®ΔώΘ©ΒΟF1Θ®-2Θ§0Θ©Θ§F2Θ®2Θ§0Θ©Θ§Υυ“‘G(
Θ§
)Θ§
¥”Εχ
=(2-
Θ§-
)Θ§
=(xΘ§y)Θ°“ρΈΣ
•
=0Θ§
Υυ“‘”–(2-
Θ§-
)•(xΘ§y)=(2-
)x+(-
)y=0Θ§Φ¥x2+y2-6x=0Θ§
”…”ΎG «ΓςNF1F2ΒΡ÷Ί–ΡΘ§Φ¥NΘ§F1Θ§F2”ΠΒ± «“ΜΗω»ΐΫ«–ΈΒΡ»ΐΗωΕΞΒψΘ§
“ρ¥ΥΥυ«σΕ·ΒψNΒΡΙλΦΘΖΫ≥ΧΈΣx2+y2-6x=0Θ®yΓΌ0Θ©Θ°
Θ®ΔσΘ©”…Θ®ΔρΘ©÷ΣΕ·ΒψNΒΡΙλΦΘΖΫ≥ΧΈΣx2+y2-6x=0Θ®yΓΌ0Θ©Θ§
Φ¥Θ®x-3Θ©2+y2=9Θ®yΓΌ0Θ©Θ°
œ‘»Μ¥ΥΙλΦΘ «“‘ΒψCΘ®3Θ§0Θ©Θ©ΈΣ‘≤–ΡΘ§ΑκΨΕr=3ΒΡ‘≤
≥ΐ»ΞΝΫΒψΘ®0Θ§0Θ©Θ§Θ®6Θ§0Θ© Θ”ύ≤ΩΖ÷ΒΡ≤ΩΖ÷«ζœΏΘ°
…ηPΘ®mΘ§nΘ©Θ§‘ρΗυΨίΤΫΟφΦΗΚΈ÷Σ ΕΒΟ|
|=|
|=
=
Θ§
cosΘΦ
Θ§
ΘΨ=cos2ΓœQPC=1-2sin2ΓœQPC=1-2•Θ®
Θ©2=1-
Θ§
¥”ΕχΗυΨίΤΫΟφœρΝΩ ΐΝΩΜΐΒΡΕ®“εΦΑΨυ÷Β≤ΜΒ» ΫΒΟΘΚ
•
=|
|•|
|•cosΘΦ
Θ§
ΘΨ=[Θ®m-3Θ©2+n2-9]•[1-
]
=[Θ®m-3Θ©2+n2]+
-27Γί2
-27=18
-27Θ°
Β±«“ΫωΒ±(m-3)2+n2=9
±Θ§»ΓΓΑ=Γ±Θ®ΓυΘ©
”…ΒψPΘ®mΘ§nΘ©‘ΎΆ÷‘≤
+
=1…œΘ®Ζ«ΕΧ÷αΕΥΒψΘ©Θ§≤Δ«“‘Ύ‘≤Θ®x-3Θ©2+y2=9ΆβΘ§
Ω…÷Σ3ΘΦ|
|Γή3+2
ΒΪ|
|ΓΌ|
|=
⇒(m-3)2+n2Γ (9Θ§13)Γ»(13Θ§17+12
]
”…”Ύ9
Γ (9Θ§13)Θ§Υυ“‘ΧθΦΰΘ®ΓυΘ©ΒΡ“Σ«σ¬ζΉψΘ°
“ρ¥Υ
•
ΒΡΉν–Γ÷ΒΈΣ18
-27Θ°
| x2 |
| a2 |
| y2 |
| b2 |
“ρΈΣM «Ά÷‘≤ΕΧ÷αΒΡ“ΜΗωΕΥΒψΘ§ΙΐF1ΒΡ÷±œΏl”κΆ÷‘≤ΫΜ”ΎAΘ§BΝΫΒψΘ§
ΓςMF1F2ΒΡΟφΜΐΈΣ4Θ§ΓςABF2ΒΡ÷ή≥ΛΈΣ8
| 2 |
Υυ“‘ 4a=8
| 2 |
| 1 |
| 2 |
Γύ
|
| 2 |
Υυ“‘Θ§Υυ«σΒΡΆ÷‘≤ΖΫ≥ΧΈΣ
| x2 |
| 8 |
| y2 |
| 4 |
Θ®ΔρΘ©…ηNΘ®xΘ§yΘ©Θ§‘ρ”…Θ®ΔώΘ©ΒΟF1Θ®-2Θ§0Θ©Θ§F2Θ®2Θ§0Θ©Θ§Υυ“‘G(
| x |
| 3 |
| y |
| 3 |
¥”Εχ
| GF2 |
| x |
| 3 |
| y |
| 3 |
| ON |
| GF2 |
| ON |
Υυ“‘”–(2-
| x |
| 3 |
| y |
| 3 |
| x |
| 3 |
| y |
| 3 |
”…”ΎG «ΓςNF1F2ΒΡ÷Ί–ΡΘ§Φ¥NΘ§F1Θ§F2”ΠΒ± «“ΜΗω»ΐΫ«–ΈΒΡ»ΐΗωΕΞΒψΘ§
“ρ¥ΥΥυ«σΕ·ΒψNΒΡΙλΦΘΖΫ≥ΧΈΣx2+y2-6x=0Θ®yΓΌ0Θ©Θ°
Θ®ΔσΘ©”…Θ®ΔρΘ©÷ΣΕ·ΒψNΒΡΙλΦΘΖΫ≥ΧΈΣx2+y2-6x=0Θ®yΓΌ0Θ©Θ§
Φ¥Θ®x-3Θ©2+y2=9Θ®yΓΌ0Θ©Θ°
œ‘»Μ¥ΥΙλΦΘ «“‘ΒψCΘ®3Θ§0Θ©Θ©ΈΣ‘≤–ΡΘ§ΑκΨΕr=3ΒΡ‘≤
≥ΐ»ΞΝΫΒψΘ®0Θ§0Θ©Θ§Θ®6Θ§0Θ© Θ”ύ≤ΩΖ÷ΒΡ≤ΩΖ÷«ζœΏΘ°
…ηPΘ®mΘ§nΘ©Θ§‘ρΗυΨίΤΫΟφΦΗΚΈ÷Σ ΕΒΟ|
| PQ |
| PR |
|
|
| (m-3)2+n2-9 |
cosΘΦ
| PQ |
| PR |
| r | ||
|
|
| 18 |
| (m-3)2+n2 |
¥”ΕχΗυΨίΤΫΟφœρΝΩ ΐΝΩΜΐΒΡΕ®“εΦΑΨυ÷Β≤ΜΒ» ΫΒΟΘΚ
| PQ |
| PR |
| PQ |
| PR |
| PQ |
| PR |
| 18 |
| (m-3)2+n2 |
=[Θ®m-3Θ©2+n2]+
| 162 |
| (m-3)2+n2 |
| 162 |
| 2 |
Β±«“ΫωΒ±(m-3)2+n2=9
| 2 |
”…ΒψPΘ®mΘ§nΘ©‘ΎΆ÷‘≤
| x2 |
| 8 |
| y2 |
| 4 |
Ω…÷Σ3ΘΦ|
| PC |
| 2 |
| PC |
| MC |
| 13 |
| 2 |
”…”Ύ9
| 2 |
“ρ¥Υ
| PQ |
| PR |
| 2 |
ΒψΤάΘΚ±ΨΧβΩΦ≤ιΆ÷‘≤ΒΡΕ®“εΓΔΖΫ≥ΧΚΆ–‘÷ Θ§ΩΦ≤ιΙλΦΘΖΫ≥ΧΒΡ«σΖ®Θ§ΩΦ≤ιΤΫΟφœρΝΩΒΡ ΐΝΩΜΐΒΡΕ®“εΚΆ–‘÷ Θ§ΩΦ≤ι÷±œΏΚΆ‘≤ΒΡΈΜ÷ΟΙΊœΒΘ§ τ”Ύ÷–ΒΒΧβΘ°

ΝΖœΑ≤αœΒΝ–¥πΑΗ
 ΆθΚσ–έ―ßΑΗΫΧ≤ΡΆξ»ΪΫβΕΝœΒΝ–¥πΑΗ
ΆθΚσ–έ―ßΑΗΫΧ≤ΡΆξ»ΪΫβΕΝœΒΝ–¥πΑΗ ΚΘΒμΩΈ ±–¬Ής“ΒΫπΑώΨμœΒΝ–¥πΑΗ
ΚΘΒμΩΈ ±–¬Ής“ΒΫπΑώΨμœΒΝ–¥πΑΗ
œύΙΊΧβΡΩ
…ηiΈΣ–ι ΐΒΞΈΜΘ§Η¥ ΐ z1=3-aiΘ§z2=1+2iΘ§»τ
«¥Ω–ι ΐΘ§‘ρ Β ΐaΒΡ÷ΒΈΣΘ®ΓΓΓΓΘ©
| z1 |
| z2 |
AΓΔ-
| ||
BΓΔ
| ||
| CΓΔ-6 | ||
| DΓΔ6 |
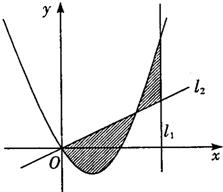 “―÷ΣΕΰ¥ΈΚ· ΐfΘ®xΘ©=3x2-3xΘ§÷±œΏl1ΘΚx=2ΚΆl2ΘΚy=3txΘ®Τδ÷–tΈΣ≥Θ ΐΘ§«“0ΘΦtΘΦ1Θ©Θ§÷±œΏl2”κΚ· ΐfΘ®xΘ©ΒΡΆΦœσ“‘ΦΑ÷±œΏl1ΓΔl2”κΚ· ΐfΘ®xΘ©ΒΡΆΦœσΥυΈß≥…ΒΡΖβ±’ΆΦ–Έ»γΆΦ÷–“θ”ΑΥυ ΨΘ§…η’βΝΫΗω“θ”Α«χ”ρΒΡΟφΜΐ÷°ΚΆΈΣSΘ®tΘ©Θ°
“―÷ΣΕΰ¥ΈΚ· ΐfΘ®xΘ©=3x2-3xΘ§÷±œΏl1ΘΚx=2ΚΆl2ΘΚy=3txΘ®Τδ÷–tΈΣ≥Θ ΐΘ§«“0ΘΦtΘΦ1Θ©Θ§÷±œΏl2”κΚ· ΐfΘ®xΘ©ΒΡΆΦœσ“‘ΦΑ÷±œΏl1ΓΔl2”κΚ· ΐfΘ®xΘ©ΒΡΆΦœσΥυΈß≥…ΒΡΖβ±’ΆΦ–Έ»γΆΦ÷–“θ”ΑΥυ ΨΘ§…η’βΝΫΗω“θ”Α«χ”ρΒΡΟφΜΐ÷°ΚΆΈΣSΘ®tΘ©Θ° »γΆΦΘ§ΥΡάβΉΕP-ABCDΒΡΒΉΟφABCD «ΨΊ–ΈΘ§≤ύΟφPAB «’ΐ»ΐΫ«–ΈΘ§AB=2Θ§BC=
»γΆΦΘ§ΥΡάβΉΕP-ABCDΒΡΒΉΟφABCD «ΨΊ–ΈΘ§≤ύΟφPAB «’ΐ»ΐΫ«–ΈΘ§AB=2Θ§BC=