题目内容
15．下列函数中是偶函数且值域为（0，+∞）的函数是（ ）| A． | y=|tanx| | B． | y=lg$\frac{x+1}{x-1}$ | C． | y=x${\;}^{\frac{1}{3}}$ | D． | y=x-2 |
分析 根据y=|tanx|的图象便可得出该函数的值域为[0，+∞），从而选项A错误，而容易判断B，C函数都是奇函数，从而B，C错误，对于D，容易判断y=x-2为偶函数，并且值域为（0，+∞），从而便得出正确选项．
解答 解：A．y=|tanx|的值域为[0，+∞），∴该选项错误；
B．解$\frac{x+1}{x-1}＞0$得，x＜-1，或x＞1；
且$lg\frac{-x+1}{-x-1}=lg\frac{x-1}{x+1}=-lg\frac{x+1}{x-1}$；
∴$y=lg\frac{x+1}{x-1}$为奇函数，∴该选项错误；
C.$y={x}^{\frac{1}{3}}$的定义域为R，且$（-x）^{\frac{1}{3}}=-{x}^{\frac{1}{3}}$；
∴该函数为奇函数，∴该选项错误；
D．y=x-2的定义域为{x|x≠0}，且（-x）-2=x-2；
∴该函数为偶函数；
且x-2＞0，即该函数的值域为（0，+∞），∴该选项正确．
故选：D．
点评 考查y=tanx和y=|tanx|的图象，奇函数和偶函数的定义及判断方法和过程，以及对数式和指数式的运算性质．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
5．已知圆的方程为x2+y2-8x+15=0，若直线y=kx+2上至少存在一点，使得以该点为圆心，半径为1的圆与圆C有公共点，则k的最小值是（ ）
| A． | $-\frac{4}{3}$ | B． | $-\frac{5}{3}$ | C． | $-\frac{3}{5}$ | D． | $-\frac{5}{4}$ |
6．
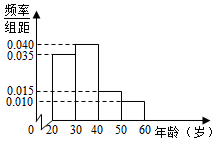某学校有120名教师，且年龄都在20岁到60岁之间，各年龄段人数按分组，其频率分布直方图如图所示，学校要求每名教师都要参加两项培训，培训结束后进行结业考试．已知各年龄段两项培训结业考试成绩优秀的人数如表示，假设两项培训是相互独立的，结业考试成绩也互不影响．
（1）若用分层抽样法从全校教师中抽取一个容量为40的样本，求从年龄段[20，30）抽取的人数；
（2）求全校教师的平均年龄；
（3）随机从年龄段[20，30）和[30，40）内各抽取1人，设这两人中两项培训结业考试成绩都优秀的人数为X，求X的概率分布和数学期望．
某学校有120名教师，且年龄都在20岁到60岁之间，各年龄段人数按分组，其频率分布直方图如图所示，学校要求每名教师都要参加两项培训，培训结束后进行结业考试．已知各年龄段两项培训结业考试成绩优秀的人数如表示，假设两项培训是相互独立的，结业考试成绩也互不影响．| 年龄分组 | A项培训成绩优秀人数 | B项培训成绩优秀人数 |
| [20，30） | 30 | 18 |
| [30，40） | 36 | 24 |
| [40，50） | 12 | 9 |
| [50，60] | 4 | 3 |
（2）求全校教师的平均年龄；
（3）随机从年龄段[20，30）和[30，40）内各抽取1人，设这两人中两项培训结业考试成绩都优秀的人数为X，求X的概率分布和数学期望．
如图所示，在平面四边形ABCD中，AB=4，AD=2，∠DAB=60°，∠BCD=120°，则四边形ABCD的面积的最大值是3$\sqrt{3}$．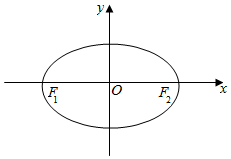
已知F1（-$\sqrt{3}$，0），F2（$\sqrt{3}$，0）为椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右焦点，点P在椭圆C上，且△PF1F2面积的最大值为$\sqrt{3}$．