题目内容
如图,
(I)求证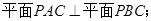
(II)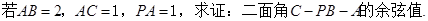
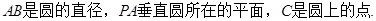

(I)求证
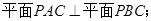
(II)
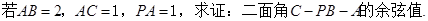
见解析
(I) ,
,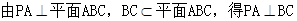
 ,
,
又因为
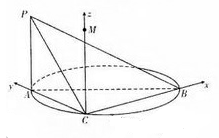
(II)解法一过C作 ,则
,则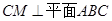 ,如图,
,如图,
以点C为坐标原点,分别以直线CB、CA、CM、为x轴,y轴,z轴
建立空间直角坐标系,因为AB=2,AC=1,所以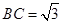
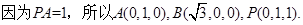 故
故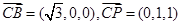
设平面BCP的法向量为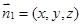 ,则
,则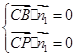 所以
所以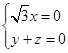 不妨令
不妨令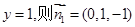
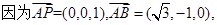 设平面ABP的法向量为
设平面ABP的法向量为 ,则
,则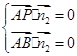 所以
所以
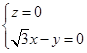 不妨令
不妨令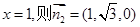

所以由题意可知二面角C-PB-A的余弦值为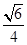

(II)解法二过C作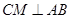 于M,因为
于M,因为
 ,
,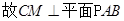 。过
。过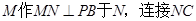 。
。
由三垂线定理得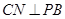 .所以
.所以 为二面角C-PB-A的平面角。
为二面角C-PB-A的平面角。
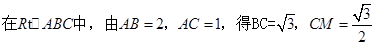 ,
,
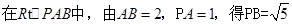 ,因为
,因为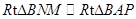
所以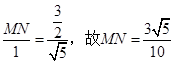 .
.
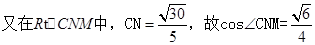 ,所以二面角C-PB-A的余弦值为
,所以二面角C-PB-A的余弦值为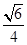 。
。
(I)本题来源于教材中的例题,主要是要表达清楚线面垂直的判定条件以及面面垂直的判定条件,学生容易漏写条件,从而丢分。(II)解法一主要是建立空间直角坐标系来解决,注重运算,特别是求好两个平面的法向量,还要注意最后的结论。解法二主要体现的是几何法求解二面角,第一步是作图找出角,第二步是证明该角为所求二面角的平面角的大小,第三步是通过计算得出该角的大小。
【考点定位】本题考查线面垂直的判断和面面垂直的判定以及求二面角的方法。
 ,
,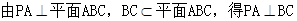
 ,
,
又因为


(II)解法一过C作
 ,则
,则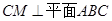 ,如图,
,如图,以点C为坐标原点,分别以直线CB、CA、CM、为x轴,y轴,z轴
建立空间直角坐标系,因为AB=2,AC=1,所以
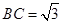
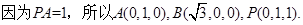 故
故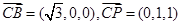
设平面BCP的法向量为
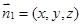 ,则
,则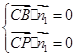 所以
所以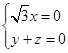 不妨令
不妨令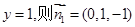
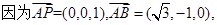 设平面ABP的法向量为
设平面ABP的法向量为 ,则
,则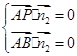 所以
所以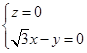 不妨令
不妨令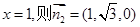

所以由题意可知二面角C-PB-A的余弦值为
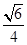

(II)解法二过C作
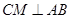 于M,因为
于M,因为
 ,
,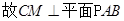 。过
。过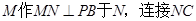 。
。由三垂线定理得
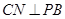 .所以
.所以 为二面角C-PB-A的平面角。
为二面角C-PB-A的平面角。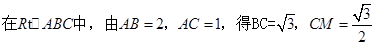 ,
,
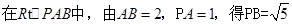 ,因为
,因为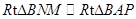
所以
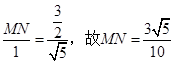 .
.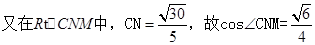 ,所以二面角C-PB-A的余弦值为
,所以二面角C-PB-A的余弦值为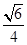 。
。(I)本题来源于教材中的例题,主要是要表达清楚线面垂直的判定条件以及面面垂直的判定条件,学生容易漏写条件,从而丢分。(II)解法一主要是建立空间直角坐标系来解决,注重运算,特别是求好两个平面的法向量,还要注意最后的结论。解法二主要体现的是几何法求解二面角,第一步是作图找出角,第二步是证明该角为所求二面角的平面角的大小,第三步是通过计算得出该角的大小。
【考点定位】本题考查线面垂直的判断和面面垂直的判定以及求二面角的方法。

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
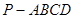 的底面
的底面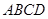 为正方形,
为正方形,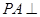 底面
底面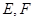 分别是
分别是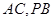 的中点.
的中点.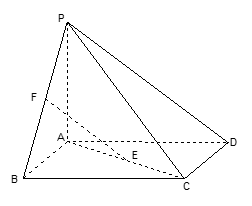
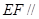 平面
平面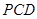 ;
;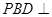 平面
平面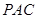 ;
;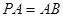 ,求
,求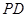 与平面
与平面 中,
中,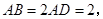
 为
为 的中点,沿
的中点,沿 将三角形
将三角形 折起,使
折起,使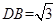 .
.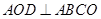 ;
; 与平面
与平面 所成角的正弦值.
所成角的正弦值.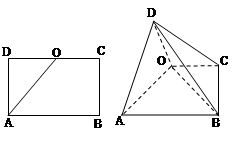
 中,
中, ,
,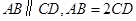 ,
, 分别为
分别为 的中点.
的中点.
 ;
; .
.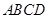 的边长为2,
的边长为2,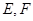 分别为边
分别为边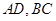 的中点,
的中点,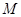 是线段
是线段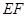 的中点,如图,把正方形沿
的中点,如图,把正方形沿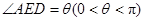 .
.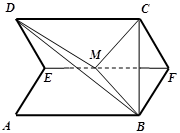
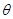 取何值,
取何值,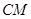 与
与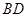 不可能垂直;
不可能垂直;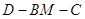 的大小为
的大小为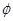 ,当
,当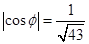 时,求
时,求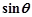 的值.
的值.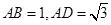 ,
,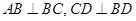 ,如图(1).把
,如图(1).把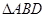 沿
沿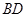 翻折,使得平面
翻折,使得平面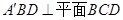 ,如图(2).
,如图(2).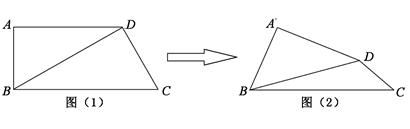
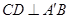 ;
;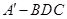 的体积;
的体积;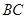 上是否存在点N,使得
上是否存在点N,使得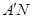
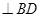 ?若存在,请求出
?若存在,请求出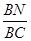 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. 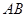 是⊙
是⊙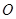 的直径,
的直径,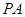 垂直于⊙
垂直于⊙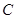 是圆周上不同于
是圆周上不同于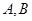 的任意一点,(1) 求证:
的任意一点,(1) 求证: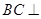 平面
平面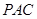 。(2) 求二面角 P-BC-A 的大小。
。(2) 求二面角 P-BC-A 的大小。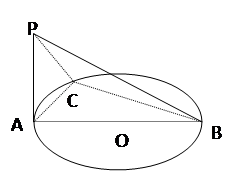
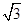 的菱形,且∠BAD=120°,且PA⊥平面ABCD,PA=
的菱形,且∠BAD=120°,且PA⊥平面ABCD,PA=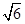 ,M,N分别为PB,PD的中点.
,M,N分别为PB,PD的中点.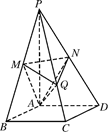
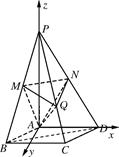
 中,
中,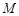 ,
,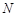 分别
分别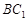 ,
,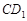 是的中点,则下列判断错误的是
是的中点,则下列判断错误的是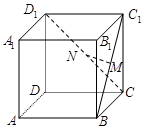
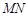 与
与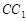 垂直
垂直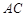 垂直
垂直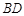 平行
平行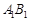 平行
平行