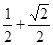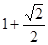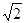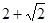题目内容
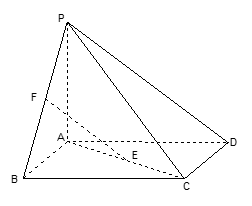
如图,四棱锥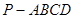 的底面
的底面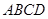 为正方形,
为正方形,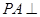 底面
底面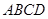 ,
,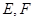 分别是
分别是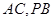 的中点.
的中点.
(1)求证: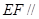 平面
平面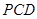 ;
;
(2)求证:平面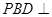 平面
平面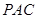 ;
;
(3)若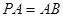 ,求
,求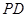 与平面
与平面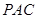 所成的角的大小.
所成的角的大小.
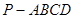 的底面
的底面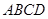 为正方形,
为正方形,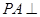 底面
底面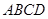 ,
,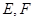 分别是
分别是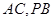 的中点.
的中点.
(1)求证:
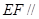 平面
平面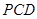 ;
;(2)求证:平面
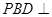 平面
平面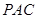 ;
;(3)若
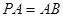 ,求
,求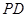 与平面
与平面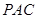 所成的角的大小.
所成的角的大小. (1)见解析;(2)见解析;(3) .
.
 .
.试题分析:(1)证明
 ;(2)证明
;(2)证明 面
面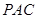 ;(3)
;(3) 是
是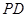 与平面
与平面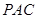 所成的角,在
所成的角,在 中求解.
中求解.试题解析:(1)如图,连结
 ,则
,则 是
是 的中点,又
的中点,又 是
是 的中点,∴
的中点,∴ .
. 又 ∵
 平面
平面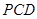 ,
, 面
面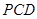
∴
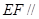 平面
平面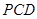 . 4分
. 4分
(2) ∵
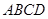 是正方形,∴
是正方形,∴  ,
,又
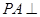 平面
平面 , 所以
, 所以 ,
,又
 ,
, 面
面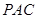 ,∴
,∴ 面
面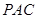 .又
.又 平面
平面 ,
,故平面

 平面
平面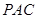 . 8分
. 8分(3)连结
 ,由第(2)问知
,由第(2)问知 面
面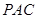 ,故
,故 是
是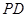 与平面
与平面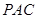 所成的角.
所成的角.∵
 ,
, , ∴
, ∴ 
在
 中,
中, , ∴
, ∴ 
所以
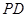 与平面
与平面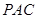 所成的角为
所成的角为 12分
12分
练习册系列答案
相关题目
 的底面
的底面 是平行四边形,且
是平行四边形,且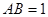 ,
,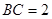 ,
,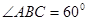 ,
,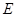 为
为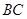 的中点,
的中点,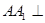 平面
平面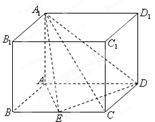
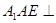 平面
平面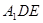 ;
;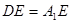 ,试求异面直线
,试求异面直线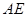 与
与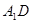 所成角的余弦值;
所成角的余弦值;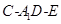 的余弦值.
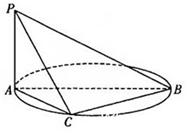
的余弦值.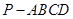 中,侧面
中,侧面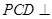 底面
底面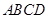 ,
,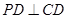 ,
,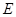 为
为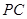 中点,底面
中点,底面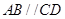 ,
,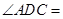
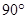 ,
,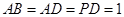 ,
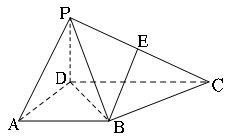
,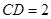 .
.
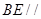 平面
平面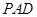 ;
;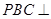 平面
平面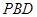 ;
;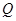 为棱
为棱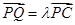 ,试确定
,试确定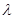 的值使得二面角
的值使得二面角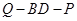 为
为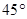 .
.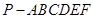 的底面是边长为1的正六边形,
的底面是边长为1的正六边形,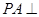 底面
底面 。
。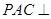 平面
平面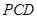 ;
;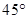 ,求三棱锥
,求三棱锥 高的大小。
高的大小。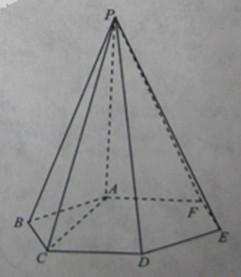
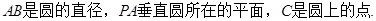
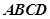 的棱长为1,M为AC的中点,P在线段DM上,则
的棱长为1,M为AC的中点,P在线段DM上,则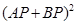 的最小值为_____________;
的最小值为_____________; 的棱长为1,动点P在正方体
的棱长为1,动点P在正方体
 ,记点P的轨迹长度为
,记点P的轨迹长度为 ,则
,则 .
.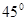 ,腰和上底均为1的等腰梯形,则这个平面图形的面积( )
,腰和上底均为1的等腰梯形,则这个平面图形的面积( )