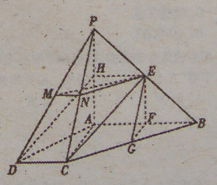
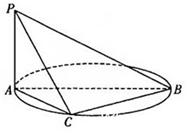
题目内容
如图,四棱锥 中,
中, ,
,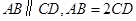 ,
, 分别为
分别为 的中点.
的中点.

(Ⅰ)求证: ;
;
(Ⅱ)求证: .
.
 中,
中, ,
,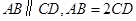 ,
, 分别为
分别为 的中点.
的中点.
(Ⅰ)求证:
 ;
;(Ⅱ)求证:
 .
.见解析
(I)取 的中点
的中点 ,连接
,连接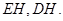
因为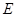 为
为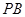 的中点,所以
的中点,所以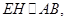
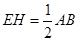 ,
,
又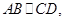
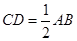 ,
,
所以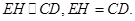
因此四边形 是平行四边形.
是平行四边形.
所以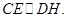
又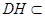 平面
平面 ,
,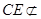 平面
平面 ,
,
因此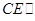 平面
平面 .
.
另解:连结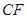 .
.
因为 为
为 的中点,所以
的中点,所以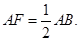
又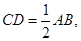 所以
所以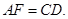
又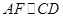 ,所以四边形
,所以四边形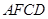 为平行四边形,因此
为平行四边形,因此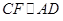 .
.
又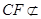 平面
平面 ,所以
,所以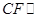 平面
平面 .
.
因为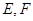 分别为
分别为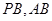 的中点,所以
的中点,所以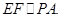
又 平面
平面 ,所以
,所以 平面
平面 .
.
因为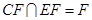 ,所以平面
,所以平面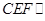 平面
平面 .
.
(II)证明 因为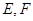 分别为
分别为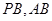 的中点,
的中点,
所以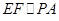 ,又因为
,又因为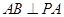 ,所以
,所以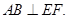
同理可证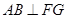 .
.
又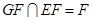 ,
,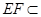 平面
平面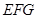 ,
,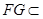 平面
平面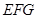 ,
,
因此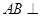 平面
平面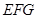 .
.
又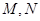 分别为
分别为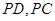 的中点,所以
的中点,所以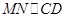 .
.
又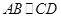 ,所以
,所以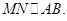
因此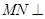 平面
平面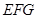 ,
,
又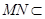 平面
平面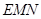 ,所以平面
,所以平面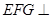 平面
平面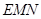 .
.

【考点定位】本题考查空间直线与平面,平面与平面间的位置关系,考查推理论证能力和空间想象能力.要证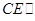 平面
平面 ,可证明平面
,可证明平面 与
与 所在的某个平面平行,不难发现平面
所在的某个平面平行,不难发现平面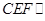 平面
平面 .证明平面
.证明平面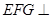 平面
平面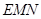 时,可选择一个平面内的一条直线(
时,可选择一个平面内的一条直线(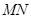 )与另一个平面垂直.线面关系与面面关系的判断离不开判定定理和性质定理,而形成结论的“证据链”依然是通过挖掘题目已知条件来实现的,如图形固有的位置关系,中点形成的三角形的中位线等,都为论证提供了丰富的素材.
)与另一个平面垂直.线面关系与面面关系的判断离不开判定定理和性质定理,而形成结论的“证据链”依然是通过挖掘题目已知条件来实现的,如图形固有的位置关系,中点形成的三角形的中位线等,都为论证提供了丰富的素材.
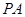 的中点
的中点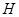 ,连接
,连接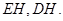
因为
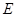 为
为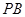 的中点,所以
的中点,所以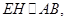
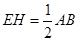 ,
,又
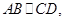
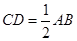 ,
,所以
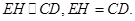
因此四边形
 是平行四边形.
是平行四边形.所以
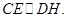
又
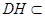 平面
平面 ,
,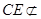 平面
平面 ,
,因此
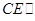 平面
平面 .
.
另解:连结
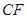 .
.因为
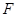 为
为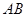 的中点,所以
的中点,所以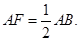
又
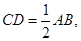 所以
所以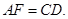
又
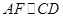 ,所以四边形
,所以四边形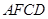 为平行四边形,因此
为平行四边形,因此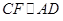 .
.又
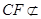 平面
平面 ,所以
,所以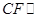 平面
平面 .
.因为
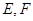 分别为
分别为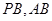 的中点,所以
的中点,所以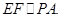
又
 平面
平面 ,所以
,所以 平面
平面 .
.因为
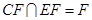 ,所以平面
,所以平面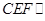 平面
平面 .
.(II)证明 因为
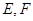 分别为
分别为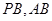 的中点,
的中点,所以
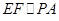 ,又因为
,又因为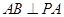 ,所以
,所以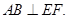
同理可证
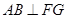 .
.又
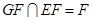 ,
,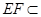 平面
平面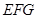 ,
,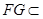 平面
平面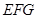 ,
,因此
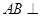 平面
平面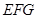 .
.又
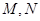 分别为
分别为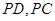 的中点,所以
的中点,所以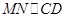 .
.又
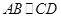 ,所以
,所以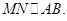
因此
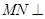 平面
平面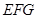 ,
,又
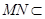 平面
平面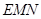 ,所以平面
,所以平面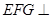 平面
平面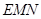 .
.
【考点定位】本题考查空间直线与平面,平面与平面间的位置关系,考查推理论证能力和空间想象能力.要证
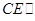 平面
平面 ,可证明平面
,可证明平面 与
与 所在的某个平面平行,不难发现平面
所在的某个平面平行,不难发现平面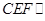 平面
平面 .证明平面
.证明平面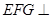 平面
平面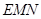 时,可选择一个平面内的一条直线(
时,可选择一个平面内的一条直线( )与另一个平面垂直.线面关系与面面关系的判断离不开判定定理和性质定理,而形成结论的“证据链”依然是通过挖掘题目已知条件来实现的,如图形固有的位置关系,中点形成的三角形的中位线等,都为论证提供了丰富的素材.
)与另一个平面垂直.线面关系与面面关系的判断离不开判定定理和性质定理,而形成结论的“证据链”依然是通过挖掘题目已知条件来实现的,如图形固有的位置关系,中点形成的三角形的中位线等,都为论证提供了丰富的素材.
练习册系列答案
相关题目
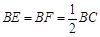 ,将△AED、△CFD分别沿DE、DF折起,使A、C两点重合于点
,将△AED、△CFD分别沿DE、DF折起,使A、C两点重合于点 ,连结A¢B.
,连结A¢B.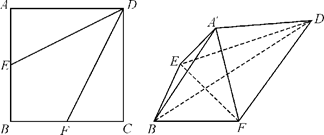
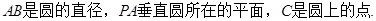
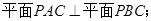
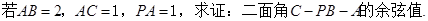
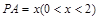 ,
,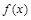 ,则函数
,则函数
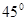 ,腰和上底均为1的等腰梯形,则这个平面图形的面积( )
,腰和上底均为1的等腰梯形,则这个平面图形的面积( )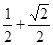
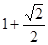
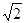
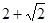
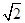 ,则 M 到面 ABC 的距离为( )
,则 M 到面 ABC 的距离为( )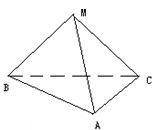
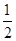
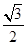
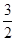
 中(图1),
中(图1), ,
,
 中点为
中点为 ,将图1沿直线
,将图1沿直线 为
为 (图2)
(图2)

 作直线
作直线 平面
平面 ,且
,且 平面
平面 ,求
,求 的长度。
的长度。 与平面
与平面 所成角的正弦值。
所成角的正弦值。 中,
中, ⊥平面
⊥平面 ,
, ⊥平面
⊥平面 ,
, ,
, 为
为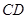 的中点.
的中点.
 ⊥平面
⊥平面 ;
; 的大小.
的大小.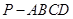 中,底面
中,底面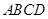 是正方形,侧面
是正方形,侧面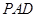
 底面
底面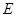 、
、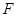 分别为
分别为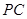 、
、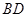 的中点.
的中点.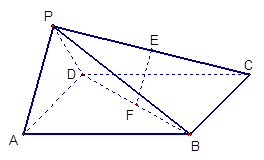
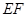 //平面
//平面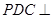 平面
平面