题目内容
(本小题满分16分)设数列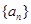 的前n项和为
的前n项和为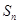 ,已知
,已知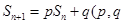 为常数,
为常数,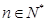 ),eg
),eg 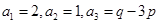
(1)求p,q的值;
(2)求数列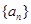 的通项公式;
的通项公式;
(3)是否存在正整数m,n,使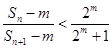 成立?若存在,求出所有符合条件的有序实数对(m,n);若不存在,说明理由。
成立?若存在,求出所有符合条件的有序实数对(m,n);若不存在,说明理由。
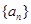 的前n项和为
的前n项和为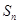 ,已知
,已知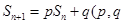 为常数,
为常数,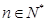 ),eg
),eg 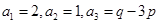
(1)求p,q的值;
(2)求数列
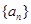 的通项公式;
的通项公式;(3)是否存在正整数m,n,使
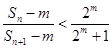 成立?若存在,求出所有符合条件的有序实数对(m,n);若不存在,说明理由。
成立?若存在,求出所有符合条件的有序实数对(m,n);若不存在,说明理由。⑴由题意,知 即
即 解之得
解之得 ……………4分
……………4分
⑵由⑴知, ,①
,①
当 时,
时, ,②
,②
① ②得,
②得, ,……………………………………………………6分
,……………………………………………………6分
又 ,所以
,所以 ,所以
,所以 是首项为
是首项为 ,公比为
,公比为 的等比数列,
的等比数列,
所以 .……………………………………………………………………8分
.……………………………………………………………………8分
⑶由⑵得, ,由
,由 ,得
,得
 ,即
,即 ,………………………10分
,………………………10分
即 ,因为
,因为 ,所以
,所以 ,
,
所以 ,且
,且 ,
,
因为 ,所以
,所以 或
或 或
或 .………………………………………………12分
.………………………………………………12分
当 时,由
时,由 得,
得, ,所以
,所以 ;
;
当 时,由
时,由 得,
得, ,所以
,所以 或
或 ;
;
当 时,由
时,由 得,
得, ,所以
,所以 或
或 或
或 ,
,
综上可知,存在符合条件的所有有序实数对 为:
为:
 .……………………………………………16分
.……………………………………………16分
 即
即 解之得
解之得 ……………4分
……………4分⑵由⑴知,
 ,①
,①当
 时,
时, ,②
,②①
 ②得,
②得, ,……………………………………………………6分
,……………………………………………………6分又
 ,所以
,所以 ,所以
,所以 是首项为
是首项为 ,公比为
,公比为 的等比数列,
的等比数列,所以
 .……………………………………………………………………8分
.……………………………………………………………………8分⑶由⑵得,
 ,由
,由 ,得
,得 ,即
,即 ,………………………10分
,………………………10分即
 ,因为
,因为 ,所以
,所以 ,
,所以
 ,且
,且 ,
,
因为
 ,所以
,所以 或
或 或
或 .………………………………………………12分
.………………………………………………12分当
 时,由
时,由 得,
得, ,所以
,所以 ;
;当
 时,由
时,由 得,
得, ,所以
,所以 或
或 ;
;当
 时,由
时,由 得,
得, ,所以
,所以 或
或 或
或 ,
,综上可知,存在符合条件的所有有序实数对
 为:
为: .……………………………………………16分
.……………………………………………16分略

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
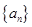 中
中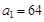 ,公比
,公比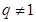 ,且
,且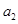 ,
,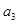 ,
,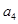 分别为某等差数列的第5项,第3项,第2项.
分别为某等差数列的第5项,第3项,第2项.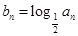 ,求数列
,求数列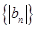 的前
的前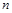 项和
项和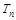 .
.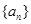 是等差数列,
是等差数列,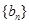 是各项都为正数的等比数列,且
是各项都为正数的等比数列,且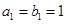 ,
,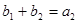 ,
,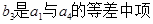 。
。  通项公式;
通项公式;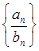 的前n项和
的前n项和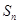 .
. 满足:
满足: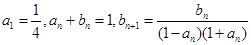 .
. ;
; ,求数列
,求数列 的通项公式;
的通项公式; ,不等式
,不等式 恒成立时,求实数
恒成立时,求实数 的取值范围.
的取值范围. 满足
满足 ,则有( )
,则有( )



 中,若
中,若 则
则 = .
= . ,则
,则 .
. 中,
中, ,且
,且 ,又设
,又设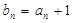 (1)求证:数列
(1)求证:数列 是等比数列; (2)求数列
是等比数列; (2)求数列 (
( ),求数列
),求数列 的前
的前 项的和
项的和