题目内容
已知数列 满足:
满足: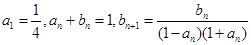 .
.
(Ⅰ)求 ;
;
(Ⅱ)设 ,求数列
,求数列 的通项公式;
的通项公式;
(Ⅲ)设 ,不等式
,不等式 恒成立时,求实数
恒成立时,求实数 的取值范围.
的取值范围.
 满足:
满足: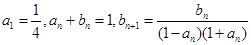 .
.(Ⅰ)求
 ;
;(Ⅱ)设
 ,求数列
,求数列 的通项公式;
的通项公式;(Ⅲ)设
 ,不等式
,不等式 恒成立时,求实数
恒成立时,求实数 的取值范围.
的取值范围.(Ⅰ) 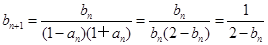
∵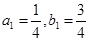 ∴
∴ ……3分
……3分
(Ⅱ)∵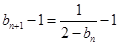 ∴
∴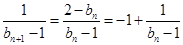
∴数列{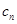 }是以-4为首项,-1为公差的等差数列.∴
}是以-4为首项,-1为公差的等差数列.∴ .--------6分
.--------6分
(Ⅲ)由于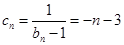 ,所以
,所以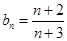 ,从而
,从而 --------7分
--------7分
∴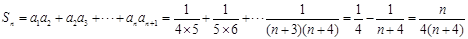
∴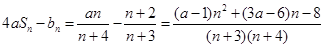 --------8分
--------8分
由条件可知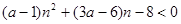 恒成立即可满足条件,设
恒成立即可满足条件,设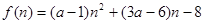
当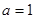 时,
时, 恒成立
恒成立
当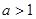 时,由二次函数的性质知不可能成立
时,由二次函数的性质知不可能成立
当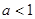 时,对称轴
时,对称轴 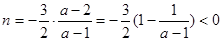
 ,
,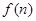 在
在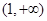 为单调递减函数.
为单调递减函数.
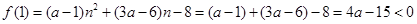 ,∴
,∴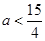 ∴
∴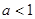 时
时 恒成立。综上知:
恒成立。综上知: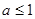 时,
时, 恒成立
恒成立
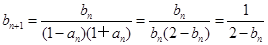
∵
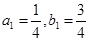 ∴
∴ ……3分
……3分(Ⅱ)∵
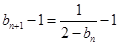 ∴
∴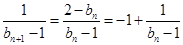
∴数列{
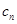 }是以-4为首项,-1为公差的等差数列.∴
}是以-4为首项,-1为公差的等差数列.∴ .--------6分
.--------6分(Ⅲ)由于
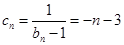 ,所以
,所以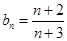 ,从而
,从而 --------7分
--------7分∴
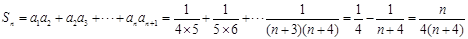
∴
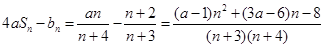 --------8分
--------8分由条件可知
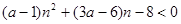 恒成立即可满足条件,设
恒成立即可满足条件,设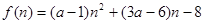
当
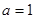 时,
时, 恒成立
恒成立当
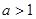 时,由二次函数的性质知不可能成立
时,由二次函数的性质知不可能成立当
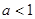 时,对称轴
时,对称轴 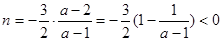
 ,
,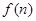 在
在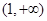 为单调递减函数.
为单调递减函数.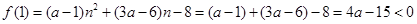 ,∴
,∴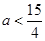 ∴
∴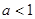 时
时 恒成立。综上知:
恒成立。综上知: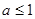 时,
时, 恒成立
恒成立略

练习册系列答案
相关题目
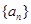 的前n项和为
的前n项和为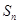 ,已知
,已知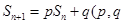 为常数,
为常数,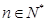 ),eg
),eg 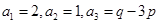
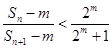 成立?若存在,求出所有符合条件的有序实数对(m,n);若不存在,说明理由。
成立?若存在,求出所有符合条件的有序实数对(m,n);若不存在,说明理由。 的前
的前 项和为
项和为 ,且
,且 ;数列
;数列 为等差数列,且
为等差数列,且 ,
,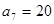 .
. ,
, 为数列
为数列 的前
的前 .
.  满足:
满足: ,
, ,
, .
. 及
及 (n
(n N*),求数列
N*),求数列 的前n项和
的前n项和 .
. ,数列
,数列 满足
满足  ,
, .
. 时,记
时,记 ,证明数列
,证明数列 是等比数列,并求
是等比数列,并求 .
.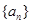 ,公差大于
,公差大于 ,且
,且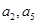 是方程
是方程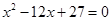 的两根,数列
的两根,数列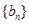 前
前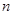 项和
项和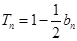 .
.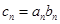 ,求证:
,求证: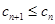
 }中,
}中, =14,前10项和
=14,前10项和 .
.
 项按原来的顺序排成一个新数列,求此数列的前
项按原来的顺序排成一个新数列,求此数列的前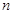 项和
项和
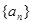 中,
中,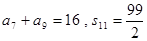 , 则
, 则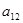 的值是
的值是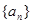 是正项数列,且
是正项数列,且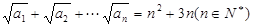
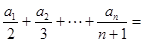 _______________
_______________