题目内容
已知函数 .
.
(1)当 时,求函数
时,求函数 的极值;
的极值;
(2)设定义在D上的函数 在点
在点 处的切线方程为
处的切线方程为 .当
.当 时,若
时,若 在D内恒成立,则称P为函数
在D内恒成立,则称P为函数 的“转点”.当
的“转点”.当 时,试问函数
时,试问函数 是否存在“转点”?若存在,求出“转点”的横坐标;若不存在,请说明理由.
是否存在“转点”?若存在,求出“转点”的横坐标;若不存在,请说明理由.
解:(I)当 时,
时,
当 ,当
,当  ,
,
所以函数 在
在 和
和 单调递增,在
单调递增,在 单调递减,
单调递减,
所以当 时,函数
时,函数 取到极大值为
取到极大值为 ,
,
当 时,函数
时,函数 取到极小值为-2. …………(6分)
取到极小值为-2. …………(6分)
(II)当 时,由函数
时,由函数 在其图像上一点
在其图像上一点 处的切线方程,
处的切线方程,
得
设
且
 …………(10分)
…………(10分)
当 时,
时, 在
在 上单调递减,
上单调递减,
所以当 时,
时, ;
;
当 时,
时, 在
在 上单调递减,
上单调递减,
所以当 时,
时, ;
;
所以 在
在 不存在 “转点”. …………(13分)
不存在 “转点”. …………(13分)
当 时,
时, ,即
,即 在
在 上是增函数.
上是增函数.
当 时,
时, 当
当 时,
时, 即点
即点 为“转点”.
为“转点”.
故函数 存在“转点”,且2是“转点”的横坐标. …………(16分)
存在“转点”,且2是“转点”的横坐标. …………(16分)

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
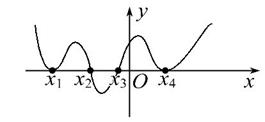 A.函数f(x)有1个极大值点,1个极小值点
A.函数f(x)有1个极大值点,1个极小值点 既有极大值又有极小值,则实数
既有极大值又有极小值,则实数 的取值范围是
的取值范围是  中,
中, ,
, ,
, ,若
,若 ,则
,则 .
. .
. 的最小正周期;
的最小正周期; 中,若
中,若 的值.
的值. 为各项都是正数的等比数列,
为各项都是正数的等比数列, 为前
为前 项和,且
项和,且 ,那么
,那么 ( )
( ) B.
B. C.
C. 或
或
 同时平分一个三角形的周长和面积,则称直线
同时平分一个三角形的周长和面积,则称直线 是公差不为0的等差数列
是公差不为0的等差数列 的前n项和,若
的前n项和,若 ,则
,则 
 (B)
(B)  (C)
(C)  (D)
(D) 