题目内容

下列命题中：
①如果两条平行线中的一条与一个平面平行，那么另一条直线也与这个平面平行；
②如果平面α，β没有公共点，则α，β异面；
③经过两条相交直线，有且只有一个平面；
④如果两个平面有三个公共点，那么这两个平面重合．
正确命题的序号有
 
（请你把所有正确命题的序号都填上）
考点：空间中直线与平面之间的位置关系
专题：空间位置关系与距离
分析：①由线面位置关系，另一条直线也可以在这个平面内 ②根据空间平面的位置关系．③、④根据公理三及其推论．
解答： 解：①错，如果两条平行直线中的一条直线与一个平面平行，那么另一条直线也与这个平面平行或在这个平面内；
②错，平面的位置关系只有平行与相交；
③正确，根据公理三及其推论；
④错，三个点如果在同一直线上，两平面可以相交．
故答案是③
点评：本题考查了线面，面面的位置关系．
练习册系列答案
相关题目
把数列{
1
n2+n
}依次按第一个括号一个数，第二个括号两个数，第三个括号三个数，第四个括号四个数，…按此规律下去，
即（
1
2
），（
1
6
，
1
12
），（
1
20
，
1
30
，
1
42
），（
1
56
，
1
72
，
1
90
，
1
110
），
则第10个括号内各数字之和为
 
．
已知10件产品，其中3件次品，不放回抽取3次，已知第一次抽到是次品，则第三次抽次品的概率是
 
．
如图所示，一个空间几何的主视图和左视图都是边长为2的正方形，俯视图是一个直径为2的圆，那么这个几何体的体积为
 
．
若f′（x0）=-3，则
lim
h→0
f(x0+h)-f(x0-3h)
h
=
 
．
已知
2+
2
3
=2
2
3
，
3+
3
8
=3
3
8
，
4+
4
15
=4
4
15
，…．，类比这些等式，若
6+
a
b
=6
a
b
（a，b均为正实数），则a+b=
 
．
设随机变量X服从正态分布N（0，1），P（X＞1）=p，则P（X＞-1）=
 
．
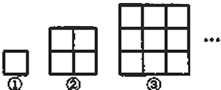如图图形都是由同样大小的正方形按一定规律组成，第①个图形中有1个正方形，第②个图形中有5个正方形，…，则第⑥个图形中正方形的个数是（　　）
A、36B、55C、70D、91
在空间内，设l，m，n是三条不同的直线，α，β，γ是三个不同的平面，则下列命题中为假命题的是（　　）
A、α⊥γ，β⊥γ，α∩β=l，则l⊥γ
B、l∥α，l∥β，α∩β=m，则l∥m
C、α∩β=l，β∩γ=m，γ∩α=n，l∥m，则l∥n
D、α⊥γ，β⊥γ，则α⊥β或α∥β

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网