题目内容
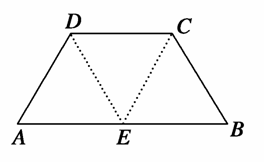
如图1,在直角梯形ABCD中,∠ADC=90°,CD∥AB,AB=4,AD=CD=2,将△ADC沿AC折起,使平面ADC⊥平面ABC,得到几何体D-ABC,如图2所示.
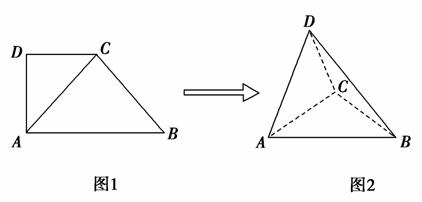
(1)求证:BC⊥平面ACD;
(2)求几何体D-ABC的体积.
(1)证明:由条件可得AC=BC=2 ,
,
从而AC2+BC2=AB2,故AC⊥BC.
又平面ADC⊥平面ABC,
平面ADC∩平面ABC=AC,
BC⊂平面ABC,∴BC⊥平面ACD.
(2)由(1)可知BC为三棱锥B-ACD的高,BC=2 ,S△ACD=2,
,S△ACD=2,
∴VB-ACD=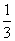 S△ACD·BC=
S△ACD·BC=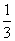 ×2×2
×2×2 =
=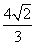 ,
,
∴几何体D-ABC的体积为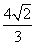 .
.

练习册系列答案
相关题目
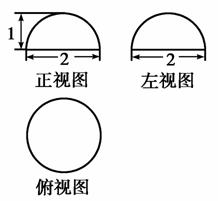
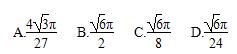
 ,若球O的体积为
,若球O的体积为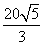 π,则这个直三棱柱的体积等于( )
π,则这个直三棱柱的体积等于( )
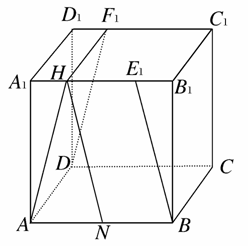
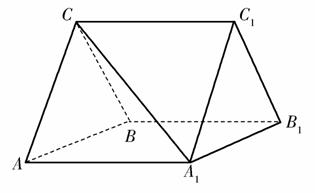
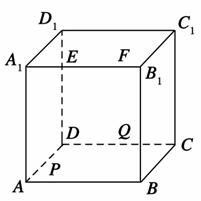
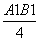 ,求BE1与DF1所成角的余弦值.
,求BE1与DF1所成角的余弦值.