题目内容
设函数f(x)=
(m∈R),方程f(x)=x有唯一解,其中m为常数,又f(a1)=
,f(an)=an+1(n∈N*).
(Ⅰ)求函数f(x)的表达式
(Ⅱ)求数列{an}的通项公式
(Ⅲ)若bn=
-7且Cn=
(n∈N+),求证:c1+c2+…+cn<n+1.
| x |
| m(x+2) |
| 2 |
| 5 |
(Ⅰ)求函数f(x)的表达式
(Ⅱ)求数列{an}的通项公式
(Ⅲ)若bn=
| 4 |
| an |
| b2n+1+b2n |
| 2bn+1bn |
考点:数列递推式
专题:点列、递归数列与数学归纳法
分析:(Ⅰ)根据方程f(x)=x有唯一解,根据一元二次方程的性质,即可求出m,则可以求函数f(x)的表达式;
(Ⅱ)根据函数的表达式,利用构造法即可求数列{an}的通项公式;
(Ⅲ)求出bn和cn的通项公式,利用裂项法进行求和,即可证明c1+c2+…+cn<n+1.
(Ⅱ)根据函数的表达式,利用构造法即可求数列{an}的通项公式;
(Ⅲ)求出bn和cn的通项公式,利用裂项法进行求和,即可证明c1+c2+…+cn<n+1.
解答:
解:(Ⅰ)∵方程f(x)=x有唯一解,
∴
=x,(m≠0),可以化简为mx(x+2)=x,
即mx2+(2m-1)x=0,
当且仅当2m-1=0,即m=
时,方程f(x)=x有唯一解,则f(x)=
.
(Ⅱ)由已知f(an)=an+1,得
=an+1,
则
=
+
,即
-
=
,
所以数列{
}是以
为首项,
为公差的等差数列,
∵f(a1)=
,∴
=
,解得a1=
,
则
=2+
(n-1)=
,
故数列{an}的通项公式an=
;
(Ⅲ)∵bn=
-7,∴bn=2n-1,
则cn=
=
=
=1+
=1+
-
,
则c1+c2+…+cn=(1+1-
)+(1+
-
)+…+(1+
-
)=n+1-
<n+1.
即不等式成立.
∴
| x |
| m(x+2) |
即mx2+(2m-1)x=0,
当且仅当2m-1=0,即m=
| 1 |
| 2 |
| 2x |
| x+2 |
(Ⅱ)由已知f(an)=an+1,得
| 2an |
| an+2 |
则
| 1 |
| an+1 |
| 1 |
| an |
| 1 |
| 2 |
| 1 |
| an+1 |
| 1 |
| an |
| 1 |
| 2 |
所以数列{
| 1 |
| an |
| 1 |
| a1 |
| 1 |
| 2 |
∵f(a1)=
| 2 |
| 5 |
| 2a1 |
| a1+2 |
| 2 |
| 5 |
| 1 |
| 2 |
则
| 1 |
| an |
| 1 |
| 2 |
| n+3 |
| 2 |
故数列{an}的通项公式an=
| 2 |
| n+3 |
(Ⅲ)∵bn=
| 4 |
| an |
则cn=
| bn+12+bn2 |
| 2bn+1bn |
| (2n+1)2+(2n-1)2 |
| 2(2n+1)(2n-1) |
| 4n2+1 |
| 4n2-1 |
| 2 |
| (2n-1)(2n+1) |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
则c1+c2+…+cn=(1+1-
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
| 1 |
| 2n+1 |
即不等式成立.
点评:本题主要考查数列的通项公式以及数列求和,根据递推熟练,通过构造法求出数列的通项公式是解决本题的关键.要求熟练掌握裂项法求和.综合性较强,有一定的难度.

练习册系列答案
相关题目
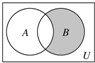 已知全集U=N,A={0,1,2},B={y|y=2x,x∈A},则图中的阴影部分所表示的集合等于( )
已知全集U=N,A={0,1,2},B={y|y=2x,x∈A},则图中的阴影部分所表示的集合等于( )| A、{0} | B、{2} |
| C、{4} | D、{2,4} |
 已知底面是矩形的四棱锥P-ABCD,PA⊥底面AC,E是PD的中点,F是AB的中点,以PB为直径的球的面积为4π,PA=1,二面角P-DC-B的大小是45°.
已知底面是矩形的四棱锥P-ABCD,PA⊥底面AC,E是PD的中点,F是AB的中点,以PB为直径的球的面积为4π,PA=1,二面角P-DC-B的大小是45°.