题目内容
在同一条道路上 甲车的速度为50km/h出发0.15h后,乙车以75km/h的速度从同一地点出发追甲车,设乙行驶的时间为t(h).
(1)写出甲,乙两车行驶的路程s与时间t的函数表达式.
(2)在同一直角坐标系中画出它们的图象.
(3)求出两条直线的交点坐标,并说明它的实际意义.
(1)写出甲,乙两车行驶的路程s与时间t的函数表达式.
(2)在同一直角坐标系中画出它们的图象.
(3)求出两条直线的交点坐标,并说明它的实际意义.
考点:函数解析式的求解及常用方法,函数的图象
专题:函数的性质及应用
分析:(1)根据甲车的速度为50km/h出发0.15h后,乙车以75km/h的速度从同一地点出发追甲车,设乙行驶的时间为th,可得S甲=50(t+0.15),S乙=75t,
(2)根据一次函数的图象和性质,可得同一直角坐标系中它们的图象.
(3)50(t+0.15)=75t,可得t值,代入可得对应s值,结合实际,可得交点坐标的实际意义.
(2)根据一次函数的图象和性质,可得同一直角坐标系中它们的图象.
(3)50(t+0.15)=75t,可得t值,代入可得对应s值,结合实际,可得交点坐标的实际意义.
解答:
解:(1)由题意得:甲,乙两车行驶的路程s与时间t的函数表达式:
S甲=50(t+0.15),S乙=75t,
(2)在同一直角坐标系中画出它们的图象如下图所示:
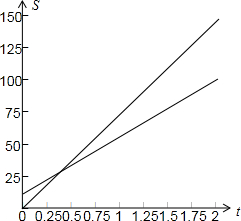
(3)由50(t+0.15)=75t得,
t=0.3,则S甲=S乙=22.5,
即两条直线的交点坐标为(0.3,22.5),
表示乙车出发后经过0.3小时后追上甲车,或行驶22.5km时,甲乙两车相遇.
S甲=50(t+0.15),S乙=75t,
(2)在同一直角坐标系中画出它们的图象如下图所示:

(3)由50(t+0.15)=75t得,
t=0.3,则S甲=S乙=22.5,
即两条直线的交点坐标为(0.3,22.5),
表示乙车出发后经过0.3小时后追上甲车,或行驶22.5km时,甲乙两车相遇.
点评:本题考查的知识点是函数解析式的求解及方法,函数的图象,函数的应用,难度不大,属于基础题.

练习册系列答案
相关题目
定义在R上的函数f(x)满足f(x+2)=
f(x),当x∈[0,2)时,f(x)=
函数g(x)=x3+3x2+m.若?s∈[-4,2),?t∈[-4,-2),不等式f(s)-g(t)≥0成立,则实数m的取值范围是( )
| 1 |
| 2 |
|
| A、(-∞,-12] | ||
| B、(-∞,-4] | ||
| C、(-∞,8] | ||
D、(-∞,
|
已知loga2<1(a>0且a≠1)则a的取值范围是( )
| A、(2,+∞) | ||
| B、(0,1) | ||
C、(0,
| ||
| D、(0,1)∪(2,+∞) |
若x∈R,则“x=1”是“|x|=1”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
设
,
是两个非零向量,则“
•
<0”是“
,
夹角为钝角”的( )
| a |
| b |
| a |
| b |
| a |
| b |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |