题目内容
已知在三棱锥A-BCD中,CA=BD=2
,CD=2
,AD=AB=BC=2,则该棱锥的外接球半径 .
| 2 |
| 3 |
考点:球的体积和表面积
专题:计算题,空间位置关系与距离
分析:证明CB⊥平面ABD,AB⊥AD,可得CD为棱锥的外接球的直径,即可得出结论.
解答:
解:∵三棱锥A-BCD中,CA=BD=2
,CD=2
,AD=AB=BC=2,
∴CB⊥AB,CB⊥BD,AB⊥AD,
∴CB⊥平面ABD,AB⊥AD,
∴CD为棱锥的外接球的直径,
∵CD=2
,
∴棱锥的外接球半径为
.
故答案为:
.
| 2 |
| 3 |
∴CB⊥AB,CB⊥BD,AB⊥AD,
∴CB⊥平面ABD,AB⊥AD,
∴CD为棱锥的外接球的直径,
∵CD=2
| 3 |
∴棱锥的外接球半径为
| 3 |
故答案为:
| 3 |
点评:本题考查棱锥的外接球半径,考查学生的计算能力,确定CD为棱锥的外接球的直径是关键.

练习册系列答案
相关题目
线面角与二面角的取值范围分别是( )
A、[0,
| ||
B、[0,
| ||
C、[0,
| ||
D、[0,
|
设f(x)是R上的偶函数,且在[0,+∞)上递增,若f(
)=0,f(log
x)<0,那么x的取值范围是( )
| 1 |
| 2 |
| 1 |
| 4 |
A、
| ||
| B、x>2 | ||
C、
| ||
D、x>2或
|
下列说法正确的是( )
| A、在平面内共线的向量,在空间不一定共线 |
| B、在空间共线的向量,在平面内不一定共线 |
| C、在平面内共线的向量,在空间一定不共线 |
| D、在空间共线的向量,在平面内一定共线 |
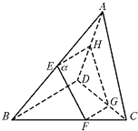 如图,空间四边形ABCD中,E、F、G分别是AB、BC、CD上,且满足AE:EB=CF:FB=2:1,CG:GD=3:1,过E、F、G的平面交AD于点H.
如图,空间四边形ABCD中,E、F、G分别是AB、BC、CD上,且满足AE:EB=CF:FB=2:1,CG:GD=3:1,过E、F、G的平面交AD于点H.