题目内容

数列{an}满足
an+1
=
a1
+
a2
+
a3
+…
an
，a1=4，则an=
 
．
考点：数列递推式,数列的求和
专题：点列、递归数列与数学归纳法
分析：根据数列的递推关系，构造方程组即可得到结论．
解答： 解：∵
an+1
=
a1
+
a2
+
a3
+…+
an
，
∴
an+2
=
a1
+
a2
+
a3
+…+
an
+
an+1
，
两式相减得
an+2
-
an+1
=
an+1
，
即
an+2
=2
an+1
，平方得an+2=4an+1，
当n=1时，
a2
=
a1
，即a2=a1=4，不满足an+2=4an+1，
∴数列{an}从第三项起是以a2=4为首项，公比q=4的等比数列，
当n≥2时，an=4•4n-2=4n-1，
则an=
4，n=1
4n-1，n≥2
．
故答案为：an=
4，n=1
4n-1，n≥2
．
点评：本题主要考查数列通项公式的计算，根据递推数列关系，构造方程组，利用作差法是解决本题的关键．
练习册系列答案
相关题目
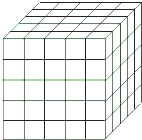如图，将一个各面都涂了油漆的正方体，切割成125个同样大小的小正方体．经过搅拌后，从中随机取出一个小正方体，则它涂了油漆的概率为
 
．
已知函数f（x）=2sin（?x-
π
6
）（0＜?＜3）图象的一条对称轴方程为x=
π
3
，若x∈[0，
π
2
]，则f（x）的取值范围是
 
．
如图所示，△ABC是边长为3的正三角形，若在每一边的两个三等分点中，各随机选取一点连成三角形，下列命题正确的是（写出所有正确命题的编号）：
 

①依此方法可能连成的三角形一共有8个；
②这些可能连成的三角形中，恰有3个是直角三角形；
③这些可能连成的三角形中，恰有2个是锐角三角形；
④这些可能连成的三角形中，恰有2个是钝角三角形．
正三角形ABC的边长为2，则
AB
•
BC
=
 
．
已知二次函数f（x）=ax2+（b-2）x+c（2a-3≤x≤1）是偶函数，则a+b=
 
．
设集合M={-2，0，1}，N={1，2，3，4，5}，映射f：M→N使对任意的x∈M，都有x+f（x）+xf（x）是奇数，则这样的映射f的个数是
 
．
已知f（x）是定义域为R的偶函数，当x≥0时，f（x）=x2-4x，那么当x＜0时，f（x）=
 
，不等式f（x+2）＜5的解集是
 
．
把一枚硬币任意抛掷两次，已知有一次出现正面，那么另一次也出现正面的概率是（　　）
A、
1
4
B、
1
3
C、
1
2
D、
2
3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网