题目内容
13.在平面直角坐标系中,记不等式组$\left\{\begin{array}{l}{y-x≥0}\\{y-{x}^{2}≤0}\\{x≤2}\end{array}\right.$所围成的平面区域的面积为S,则S为( )| A. | $\frac{5}{6}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{6}$ | D. | 1 |
分析 由题意作平面区域,从而利用定积分的几何意义求解即可.
解答 解:由题意作平面区域如下, ,
,
结合图象可知,A(1,1),B(2,4);
故S=${∫}_{1}^{2}$x2dx-$\frac{1}{2}$×(1+2)×1
=$\frac{1}{3}$x3|$\left.\begin{array}{l}{2}\\{1}\end{array}\right.$-$\frac{3}{2}$
=$\frac{8}{3}$-$\frac{1}{3}$-$\frac{3}{2}$=$\frac{5}{6}$;
故选:A.
点评 本题考查了定积分的几何意义的应用及数形结合的思想应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.一个空间几何体的三视图如图所示,则几何体的体积为( )


| A. | 2 | B. | $\frac{8}{3}$ | C. | 3 | D. | $\frac{10}{3}$ |
18.已知幂函数y=f(x)的图象经过点$(4,\frac{1}{2})$,且f(a+1)<f(10-2a),则实数a的取值范围是( )
| A. | (-1,5) | B. | (-∞,3) | C. | (3,+∞) | D. | (3,5) |
2.某几何体的三视图如图所示,则该几何体的表面积为( )
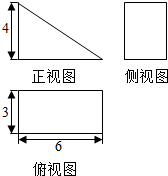

| A. | 36 | B. | $54+6\sqrt{13}$ | C. | $54+12\sqrt{5}$ | D. | $30+6\sqrt{73}$ |
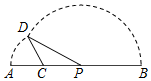 如图,线段AB=8,点C在线段AB上,且AC=2,P为线段CB上一动点,点A绕点C旋转后与点B绕点P旋转后重合于点D.设CP=x,△CPD的面积为f(x).则f(x)的定义域为(2,4); f′(x)=0的解是3.
如图,线段AB=8,点C在线段AB上,且AC=2,P为线段CB上一动点,点A绕点C旋转后与点B绕点P旋转后重合于点D.设CP=x,△CPD的面积为f(x).则f(x)的定义域为(2,4); f′(x)=0的解是3.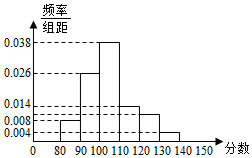 某中学一名高三数学教师,对其所教的文科班50名同学的一次数学成绩进行了统计,全年级文科数学平均分是100分,这个班数学成绩的频率分布直方图如图:(总分150分)
某中学一名高三数学教师,对其所教的文科班50名同学的一次数学成绩进行了统计,全年级文科数学平均分是100分,这个班数学成绩的频率分布直方图如图:(总分150分)