题目内容
已知an=
+
+…+
(n=1,2,3…),则an+1= .
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| 2n |
考点:数列的概念及简单表示法
专题:点列、递归数列与数学归纳法
分析:由已知,只要将变量n换为n+1即可.
解答:
解:∵已知an=
+
+…+
(n=1,2,3…),
∴an+1=
+
+…+
+
.
故答案为:
+
+…+
+
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| 2n |
∴an+1=
| 1 |
| n+2 |
| 1 |
| n+3 |
| 1 |
| 2n+1 |
| 1 |
| 2(n+1) |
故答案为:
| 1 |
| n+2 |
| 1 |
| n+3 |
| 1 |
| 2n+1 |
| 1 |
| 2(n+1) |
点评:本题考查了数列的通项公式;数列的通项是n为自变量,数列的项为函数值的一个特殊的函数,当自变量由n变为n+1时,注意项数的变化.

练习册系列答案
相关题目
已知cosα=-
,则sin(30°+α)+sin(30°-α)的值为( )
| 1 |
| 2 |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
若a、b、c、d、x、y 是正实数,且P=
+
,Q=
•
,则( )
| ab |
| cd |
| ax+cy |
|
| A、P=Q |
| B、P3=Q |
| C、P≥Q |
| D、P>Q |
函数f(x)=
的定义域为( )
| lnx+1 | ||
|
| A、(-1,+∞) |
| B、(-∞,1) |
| C、(0,1) |
| D、(-1,1] |
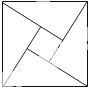 2002年8月,在北京召开的国际数学家大会会标如图所示,会标是以我国古代数学家赵爽的弦图为基础设计的.弦图是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形,若直角三角形中较小的锐角为θ,大正方形的面积是1,小正方形的面积是
2002年8月,在北京召开的国际数学家大会会标如图所示,会标是以我国古代数学家赵爽的弦图为基础设计的.弦图是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形,若直角三角形中较小的锐角为θ,大正方形的面积是1,小正方形的面积是