题目内容
15.已知函数f(x)=$\left\{\begin{array}{l}{x,x≤1}\\{(\frac{1}{2})^{x-1},x>1}\end{array}\right.$,则f(f(2))=$\frac{1}{2}$,不等式f(x-3)<f(2)的解集为{x|x<$\frac{7}{2}$或x>5}.分析 根据分段函数的解析式直接代值计算即可求出f(f(2)),分类讨论,即可求出不等式f(x-3)<f(2)的解集.
解答 解:f(2)=$(\frac{1}{2})^{2-1}$=$\frac{1}{2}$,f($\frac{1}{2}$)=$\frac{1}{2}$,
∴f(f(2))=$\frac{1}{2}$,
当x-3>1时,即x>4时,$(\frac{1}{2})^{x-3-1}$<$\frac{1}{2}$,解得x>5,
当x-3≤1时,即x≤4时,x-3<$\frac{1}{2}$,解得x<$\frac{7}{2}$,
综上所述不等式f(x-3)<f(2)的解集为{x|x<$\frac{7}{2}$或x>5}
故答案为:$\frac{1}{2}$,{x|x<$\frac{7}{2}$或x>5}.
点评 本题考查了分段函数的函数值的问题,以及不等式的解集的问题,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.下面各组函数中为相同函数的是( )
| A. | f(x)=$\sqrt{(x-1)^{2}}$,g(x)=x-1 | B. | f(x)=$\sqrt{{x}^{2}-1}$,g(x)=$\sqrt{x+1}$•$\sqrt{x-1}$ | ||
| C. | f(x)=ln ex与g(x)=elnx | D. | f(x)=(x-1)0与g(x)=$\frac{1}{(x-1)^{0}}$ |
10.已知三棱柱ABC-A1B1C1的底面是锐角三角形,则存在过点A的平面( )
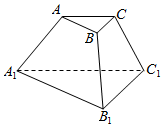

| A. | 与直线BC和直线A1B1都平行 | B. | 与直线BC和直线A1B1都垂直 | ||
| C. | 与直线BC平行且直线A1B1垂直 | D. | 与直线BC和直线A1B1所成角相等 |
20.函数f(x)=x2-ln|x|的大致图象为( )
| A. | 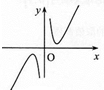 | B. | 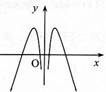 | C. | 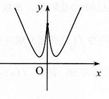 | D. | 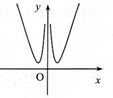 |
4.为提高在校学生的安全意识,防止安全事故的发生,学校拟在高三年级的1-10班中随机抽取3个班进行网上安全知识竞赛,则选择的3个班恰好为连续编号的3个班的概率是( )
| A. | $\frac{1}{10}$ | B. | $\frac{3}{25}$ | C. | $\frac{1}{15}$ | D. | $\frac{1}{30}$ |