题目内容
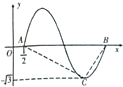 已知函数f(x)=
已知函数f(x)=| 3 |
| π |
| 2 |
| π |
| 2 |
(Ⅰ)求ω与φ的值;
(Ⅱ)不画图,说明函数y=f(x)的图象经过怎样的变化可得到y=sinx的图象.
考点:由y=Asin(ωx+φ)的部分图象确定其解析式,函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:(1)设函数f(x)=
sin(ωx+φ)的周期为T,依题意AC2+CH2=AH2,可求得T=
=4,于是可求得ω,继而可求得φ;
(2)由(1)可知f(x)=
sin(
x-
),利用函数y=Asin(ωx+φ)的图象变换即可说明函数y=f(x)的图象经过怎样的变化可得到y=sinx的图象.
| 3 |
| 2π |
| ω |
(2)由(1)可知f(x)=
| 3 |
| π |
| 2 |
| π |
| 4 |
解答:
解:(1)设函数f(x)=
sin(ωx+φ)的周期为T,则A(
,0),C(
+
,-
),H(
+T,0),
∵∠ACB=
,
∴AC2+CH2=AH2,即
T2+3+
+3=T2,解得:T=4,
∴ω=
=
.
又
ω+φ=2kπ(k∈Z),
∴φ=2kπ-
(k∈Z),又|φ|<
,
∴φ=-
.
(2)由(1)知,f(x)=
sin(
x-
),
将f(x)=
sin(
x-
)的图象向左平移
个单位,得到y=
sin
x的图象,再将得到的图象的横坐标伸长为原来的
倍(纵坐标不变),得到y=
sinx的图象,
最后将y=
sinx的图象的纵坐标变为原来的
(横坐标不变),得到y=sinx的图象.
| 3 |
| 1 |
| 2 |
| 3T |
| 4 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
∵∠ACB=
| π |
| 2 |
∴AC2+CH2=AH2,即
| 9 |
| 16 |
| T2 |
| 16 |
∴ω=
| 2π |
| 4 |
| π |
| 2 |
又
| 1 |
| 2 |
∴φ=2kπ-
| π |
| 4 |
| π |
| 2 |
∴φ=-
| π |
| 4 |
(2)由(1)知,f(x)=
| 3 |
| π |
| 2 |
| π |
| 4 |
将f(x)=
| 3 |
| π |
| 2 |
| π |
| 4 |
| 1 |
| 2 |
| 3 |
| π |
| 2 |
| π |
| 2 |
| 3 |
最后将y=
| 3 |
| ||
| 3 |
点评:本题主要考查了三角函数y=Asin(ωx+φ)的图象解析式的确定,考查正弦函数的图象和性质,考查了三角函数的图象变换理论,属于基本知识的考查.

练习册系列答案
相关题目
 (Ⅰ) 如图,一个扇形OAB的面积是1cm2,它的周长是4cm,求圆心角的弧度数和弦长AB.
(Ⅰ) 如图,一个扇形OAB的面积是1cm2,它的周长是4cm,求圆心角的弧度数和弦长AB.(Ⅱ) 已知f(x)=-sin2x+sinx+a,若1≤f(x)≤
| 17 |
| 4 |
在△ABC中,已知a=
,b=2,A=30°,则角B=( )
| 2 |
| A、45° |
| B、60° |
| C、45°或135° |
| D、60°或120° |
函数f(x)=
的定义域是( )
| x2-4x+3 |
| A、x∈R |
| B、x∈(0,3) |
| C、x∈(1,3) |
| D、x∈(-∞,1]∪[3,+∞) |
已知函数f(x)=ex-
(x<0)与g(x)=ln(x+a)图象上存在关于y轴对称的点,则实数a的取值范围是( )
| 1 |
| 2 |
A、(-∞,
| ||||||
B、(-∞,
| ||||||
C、(-
| ||||||
D、(-
|
圆心在直线y=x上且与x轴相切于点(1,0)的圆的方程为( )
| A、(x-1)2+y2=1 |
| B、(x-1)2+(y-1)2=1 |
| C、(x+1)2+(y-1)2=1 |
| D、(x+1)2+(y+1)2=1 |
在△ABC中,已知sinA+cosA=
,则角A为( )
| 1 |
| 5 |
| A、锐角 | B、直角 |
| C、钝角 | D、锐角或钝角 |