题目内容
对于函数f(x)(x∈D),若x∈D时,恒有 >
> 成立,则称函数
成立,则称函数 是D上的J函数.
是D上的J函数.
(Ⅰ)当函数f(x)=m lnx是J函数时,求m的取值范围;
lnx是J函数时,求m的取值范围;
(Ⅱ)若函数g(x)为(0,+∞)上的J函数,
试比较g(a)与 g(1)的大小;
g(1)的大小;
求证:对于任意大于1的实数x1,x2,x3, ,xn,均有g(ln(x1+x2+ +xn))
>g(lnx1)+g(lnx2)+ +g(lnxn).
(Ⅰ) ;(Ⅱ)①
;(Ⅱ)① ,②先征得
,②先征得 ,
, 取不同的值得到的式子累加即可得证.
取不同的值得到的式子累加即可得证.
解析试题分析:(Ⅰ)先求得 ,再由
,再由 >
> 得
得 ,解得
,解得 ;(Ⅱ)①构造函数
;(Ⅱ)①构造函数 ,证明
,证明 为
为 上的增函数,再讨论就可得到
上的增函数,再讨论就可得到 ,②先证得
,②先证得 ,
,
即得 ,
,
整理得 ,
,
同理可得类似的的等式,累加即可得证.
试题解析:(Ⅰ)由 ,可得
,可得 ,
,
因为函数 是
是 函数,所以
函数,所以 ,即
,即 ,
,
因为 ,所以
,所以 ,即
,即 的取值范围为
的取值范围为 . (3分)
. (3分)
(Ⅱ)①构造函数 ,则
,则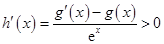 ,可得
,可得 为
为 上的增函数,当
上的增函数,当 时,
时, ,即
,即 ,得
,得 ;
;
当 时,
时, ,即
,即 ,得
,得 ;
;
当 时,
时, ,即
,即 ,得
,得 . (6分)
. (6分)
②因为 ,所以
,所以 ,
,
由①可知 ,
,
所以 ,整理得
,整理得 ,
,
同理可得 , ,
, , .
.
把上面 个不等式同向累加可得[
个不等式同向累加可得[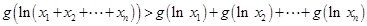 . (12分)
. (12分)
考点:1.恒成立问题;2.导数在求函数单调性、最值的应用;3.不等式.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
 ,其中
,其中
 的奇偶性与单调性(不要求证明);
的奇偶性与单调性(不要求证明); 的定义域为
的定义域为 ,求满足不等式
,求满足不等式 的实数
的实数 的取值集合;
的取值集合; 时,
时, 的值恒为负,求
的值恒为负,求 的取值范围.
的取值范围.
 ,解不等式
,解不等式 ;
; 时,若
时,若
 ,使得不等式
,使得不等式 成立,求实数
成立,求实数 的取值范围.
的取值范围. ,
, .
. 的单调区间;
的单调区间; 时,函数
时,函数 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; 满足
满足 ,求证:
,求证: .
. 的定义域是
的定义域是 ,
, 是
是 在
在 的单调区间;
的单调区间;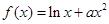 ,求
,求 的取值范围;
的取值范围; 是
是 ,求证:
,求证: .
.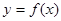 是定义域为
是定义域为 的奇函数,且当
的奇函数,且当 时,
时, ,(
,( 。
。 的值;并求函数
的值;并求函数
 上是增函数。
上是增函数。 .
.
 .
. ,求
,求 的单调区间及
的单调区间及 ,求
,求 与
与 的大小
的大小 ,并证明你的结论.
,并证明你的结论. ,求f(x)和g(x)的解析式。
,求f(x)和g(x)的解析式。