题目内容

8．已知函数f（x）=$\frac{x}{{e}^{x}}$+sin2x，则$\underset{lim}{△x→0}$$\frac{f（△x）-f（0）}{△x}$=3．

分析 根据条件得出$\underset{lim}{△x→0}$$\frac{f（△x）-f（0）}{△x}$=f′（0），运用导数运算公式求解即可．

解答 解：∵$\underset{lim}{△x→0}$$\frac{f（△x）-f（0）}{△x}$=f′（0），
函数f（x）=$\frac{x}{{e}^{x}}$+sin2x，
∴f′（x）=$\frac{1-x}{{e}^{x}}$+2cos2x，
∴f′（0）=1+2=3，
故答案为：3

点评 本题简单的考查了导数的概念，关键理解极限给出式子，导数的运用公式，属于中档题．

练习册系列答案
相关题目
16．己知函数f（x）=$\left\{\begin{array}{l}{cos\frac{π}{4}x，x≤2000}\\{x-14，x＞2000}\end{array}\right.$，则f[f（2014）]=（　　）
A．1B．-1C．0D．$\frac{\sqrt{2}}{2}$
19．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的焦距为2，左右焦点分别为F1，F2，以原点O为圆心，以椭圆C的半短轴长为半径的圆与直线3x-4y+5=0相切．
（Ⅰ）求椭圆C的方程；
（Ⅱ）设不过原点的直线l：y=kx+m与椭圆C交于A，B两点．
（i）若直线AF2与BF2的斜率分别为k1，k2，且k1+k2=0，求证：直线l过定点，并求出该定点的坐标；
（ii）若直线l的斜率是直线OA，OB斜率的等比中项，求△OAB面积的取值范围．
16．执行如图所示的程序框图，如果输入的t=50，则输出的n=（　　）
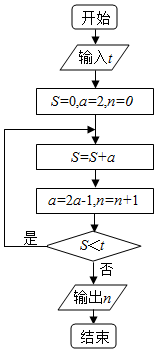
A．5B．6C．7D．8
3．执行如图所示的程序框图，则该程序运行后输出的i值为（　　）
A．8B．9C．10D．11
13．已知△ABC的内角A，B，C的对边分别为a，b，c，$\overrightarrow{m}$=（$\frac{a}{sin（A+B）}$，c-2b），$\overrightarrow{n}$=（sin2C，1），且满足$\overrightarrow{m}•\overrightarrow{n}$=0．
（1）求∠A的大小；
（2）若a=1，求△ABC周长的取值范围．
20．二次项（2x-$\frac{1}{2x}$）6展开式中的常数项为-20．
17．已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$（a＞b＞0）的短轴长为2，离心率$e=\frac{{\sqrt{2}}}{2}$．
（1）求椭圆C的方程；
（2）若斜率为k的直线过点M（2，0），且与椭圆C相交于A，B两点．试求k为何值时，三角形OAB是以O为直角顶点的直角三角形．
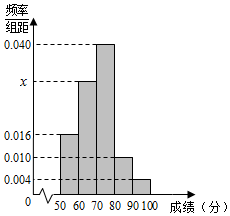18．某中学举行了一次“环保知识竞赛”活动．为了了解本次竞赛学生成绩情况，从中抽取了部分学生的分数（得分取正整数，满分为100分）作为样本（样本容量为n）进行统计．按照[50，60），[60，70），[70，80），[80，90），[90，100]的分组作出如图所示的频率分布直方图，但由于不慎丢失了部分数据．已知得分在[50，60）的有8人，在[90，100]的有2人，由此推测频率分布直方图中的x=0.03．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网