题目内容
15.函数y=($\frac{1}{2}$)${\;}^{{x}^{2}-1}$,其中x∈[-2,1]的值域为[$\frac{1}{8}$,2].分析 根据x的范围即可求出x2-1的范围,根据指数函数的单调性便可求出原函数的值域.
解答 解:x∈[-2,1];
∴x2-1∈[-1,3];
∴$(\frac{1}{2})^{{x}^{2}-1}∈[\frac{1}{8},2]$;
∴原函数的值域为$[\frac{1}{8},2]$.
故答案为:$[\frac{1}{8},2]$.
点评 考查函数值域的概念及求法,二次函数及指数函数的值域的求法.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案
相关题目
9.复数z=$\frac{(i-1)^{2}+1}{{i}^{2}}$的实部为( )
| A. | 0 | B. | -1 | C. | 1 | D. | 2 |
10.满足条件{1,3}∪A={1,3,5}所有集合A的个数是( )
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
5.已知过抛物线G:y2=2px(p>0)焦点F的直线l与抛物线G交于M、N两点(M在x轴上方),满足$\overrightarrow{MF}=3\overrightarrow{FN}$,$|{MN}|=\frac{16}{3}$,则以M为圆心且与抛物线准线相切的圆的标准方程为( )
| A. | ${({x-\frac{1}{3}})^2}+{({y-\frac{{2\sqrt{3}}}{3}})^2}=\frac{16}{3}$ | B. | ${({x-\frac{1}{3}})^2}+{({y-\frac{{\sqrt{3}}}{3}})^2}=\frac{16}{3}$ | ||
| C. | ${({x-3})^2}+{({y-2\sqrt{3}})^2}=16$ | D. | ${({x-3})^2}+{({y-\sqrt{3}})^2}=16$ |
 如图,棱锥P-ABCD的底面ABCD是矩形,PA⊥面ABCD,PA=AD=4,BD=4$\sqrt{2}$,E为PD的中点.
如图,棱锥P-ABCD的底面ABCD是矩形,PA⊥面ABCD,PA=AD=4,BD=4$\sqrt{2}$,E为PD的中点.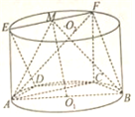 在如图所示的圆柱O1O2中,等腰梯形ABCD内接于下底面圆O1,AB∥CD,且AB为圆O1的直径,EA和FC都是圆柱O1O2的母线,M为线段EF的中点.
在如图所示的圆柱O1O2中,等腰梯形ABCD内接于下底面圆O1,AB∥CD,且AB为圆O1的直径,EA和FC都是圆柱O1O2的母线,M为线段EF的中点.