题目内容
9. 如图所示,单位位圆上的两个向量$\overrightarrow{a},\overrightarrow{b}$相互垂直,若向量$\overrightarrow{c}$满足($\overrightarrow{c}-\overrightarrow{a}$)•($\overrightarrow{c}-\overrightarrow{b}$)=0,则|$\overrightarrow{c}$|的取值范围是( )
如图所示,单位位圆上的两个向量$\overrightarrow{a},\overrightarrow{b}$相互垂直,若向量$\overrightarrow{c}$满足($\overrightarrow{c}-\overrightarrow{a}$)•($\overrightarrow{c}-\overrightarrow{b}$)=0,则|$\overrightarrow{c}$|的取值范围是( )| A. | [0,1] | B. | [0,$\sqrt{2}$] | C. | [1,$\sqrt{2}$] | D. | [1,2] |
分析 先由条件可得出$\overrightarrow{a}•\overrightarrow{b}=0$,|$\overrightarrow{a}+\overrightarrow{b}$|=$\sqrt{2}$,这样便可由$(\overrightarrow{c}-\overrightarrow{a})•(\overrightarrow{c}-\overrightarrow{b})=0$得出$|\overrightarrow{c}|=\sqrt{2}cos<\overrightarrow{c},\overrightarrow{a}+\overrightarrow{b}>$,从而得出$|\overrightarrow{c}|$的取值范围.
解答 解:由条件,$\overrightarrow{a}•\overrightarrow{b}=0$,$|\overrightarrow{a}+\overrightarrow{b}|=\sqrt{{\overrightarrow{a}}^{2}+2\overrightarrow{a}•\overrightarrow{b}+{\overrightarrow{b}}^{2}}=\sqrt{2}$;
∵$(\overrightarrow{c}-\overrightarrow{a})•(\overrightarrow{c}-\overrightarrow{b})=0$;
∴${\overrightarrow{c}}^{2}-\overrightarrow{c}•(\overrightarrow{a}+\overrightarrow{b})=0$;
∴$|\overrightarrow{c}|=\sqrt{2}cos<\overrightarrow{c},\overrightarrow{a}+\overrightarrow{b}>$;
∴$0≤|\overrightarrow{c}|≤\sqrt{2}$;
∴$|\overrightarrow{c}|$的取值范围为$[0,\sqrt{2}]$.
故选B.
点评 考查向量垂直的充要条件,单位向量的概念,向量数量积的运算及计算公式.

 阅读快车系列答案
阅读快车系列答案| A. | a≥1 | B. | a≤1 | C. | a≥-1 | D. | -1≤a≤0 |
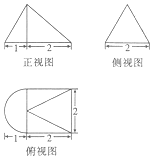 某几何体的三视图如图所示,且其侧视图是一个等边三角形,则这个几何体的表面积为( )
某几何体的三视图如图所示,且其侧视图是一个等边三角形,则这个几何体的表面积为( )| A. | $\frac{(8+π)\sqrt{3}}{2}$ | B. | $\frac{(8+π)\sqrt{3}}{6}$ | C. | $\frac{π}{2}$+4+$\frac{5}{2}$$\sqrt{3}$ | D. | $\frac{3}{2}$π+8+$\sqrt{7}$ |
| A. | {x|-2≤x≤0} | B. | {x|2≤x≤4} | C. | {x|0≤x≤4} | D. | {x|x≤-2} |
| A. | $\frac{8}{5}$ | B. | $\frac{6}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{2}{5}$ |