题目内容
如图,已知椭圆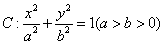 的离心率是
的离心率是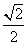 ,
,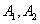 分别是椭圆
分别是椭圆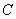 的左、右两个顶点,点
的左、右两个顶点,点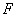 是椭圆
是椭圆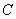 的右焦点。点
的右焦点。点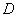 是
是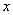 轴上位于
轴上位于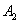 右侧的一点,且满足
右侧的一点,且满足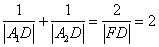 。
。
(1)求椭圆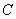 的方程以及点
的方程以及点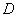 的坐标;
的坐标;
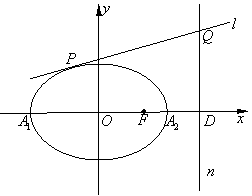
(2)过点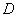 作
作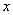 轴的垂线
轴的垂线 ,再作直线
,再作直线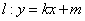 与椭圆
与椭圆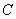 有且仅有一个公共点
有且仅有一个公共点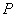 ,直线
,直线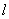 交直线
交直线 于点
于点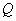 。求证:以线段
。求证:以线段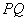 为直径的圆恒过定点,并求出定点的坐标。
为直径的圆恒过定点,并求出定点的坐标。
 |
解:(1) ,设
,设 ,由
,由 有
有 ,又
,又 ,
, ,于是
,于是
 ,又
,又 ,
,
 ,又
,又 ,
, ,椭圆
,椭圆 ,且
,且 。
。
(2) ,设
,设 ,由
,由

 ,
,
由于 (*),
(*),
而由韦达定理: ,
,
 ,
, ,
,
设以线段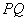 为直径的圆上任意一点
为直径的圆上任意一点 ,由
,由 有
有
 由对称性知定点在
由对称性知定点在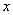 轴上,令
轴上,令 ,取
,取 时满足上式,故过定点
时满足上式,故过定点 。
。

练习册系列答案
相关题目
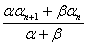 ,n∈N*,其中常数α,β均为非零实数,且α+β≠0.
,n∈N*,其中常数α,β均为非零实数,且α+β≠0.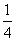 , a1=1,a2=
, a1=1,a2=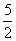 ,求证:数列{| an+1-an-1|} (n∈N*,n≥2)与数列{n+
,求证:数列{| an+1-an-1|} (n∈N*,n≥2)与数列{n+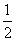 } (n∈N*)中没有相同数值的项.
} (n∈N*)中没有相同数值的项. 的定义域为 .
的定义域为 . 的右焦点为
的右焦点为 且倾斜角为
且倾斜角为 的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是( )
的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是( ) B.
B. C.
C. D.
D.
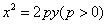 的焦点为
的焦点为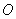 ,准线为
,准线为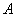 作
作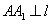 于点
于点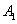 ,以线段
,以线段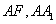 为邻边作平行四边形
为邻边作平行四边形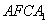 ,连接直线
,连接直线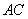 交
交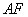 交抛物线于另一点
交抛物线于另一点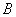 。若
。若 的面积为
的面积为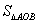 ,
,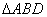 的面积为
的面积为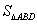 ,则
,则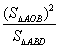 的最大值为____________。
的最大值为____________。 上单调递减(2)最小正周期为
上单调递减(2)最小正周期为 (3)是奇函数
(3)是奇函数 B.
B. C.
C. D.
D.
 ,则行列式
,则行列式
 = .
= .