题目内容
2.若$\overrightarrow{AB}$$•\overrightarrow{AC}$=-1,|$\overrightarrow{AB}$|=2,|$\overrightarrow{AC}$|=1,则($\frac{1}{2}$$\overrightarrow{AB}$-$\overrightarrow{AC}$)•($\overrightarrow{AB}$+$\overrightarrow{AC}$)的值为( )| A. | $\frac{3}{8}$ | B. | $\frac{3}{4}$ | C. | $\frac{5}{4}$ | D. | $\frac{3}{2}$ |
分析 根据平面向量数量积运算法则,计算即可.
解答 解:$\overrightarrow{AB}$$•\overrightarrow{AC}$=-1,|$\overrightarrow{AB}$|=2,|$\overrightarrow{AC}$|=1,
∴($\frac{1}{2}$$\overrightarrow{AB}$-$\overrightarrow{AC}$)•($\overrightarrow{AB}$+$\overrightarrow{AC}$)=$\frac{1}{2}$${\overrightarrow{AB}}^{2}$-$\frac{1}{2}$$\overrightarrow{AB}$•$\overrightarrow{AC}$-${\overrightarrow{AC}}^{2}$
=$\frac{1}{2}$×22-$\frac{1}{2}$×(-1)-12
=$\frac{3}{2}$.
故选:D.
点评 本题考查了平面向量数量积的运算问题,是基础题.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
13.若复数z满足$(1+i)z=|{\sqrt{3}+i}|$,则在复平面内,$\overline z$对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
18.函数f(x)=x3+x2+5ax-1存在极值点的充要条件是( )
| A. | a$≤\frac{1}{15}$ | B. | a<$\frac{1}{15}$ | C. | a$≥\frac{1}{15}$ | D. | a>$\frac{1}{15}$ |
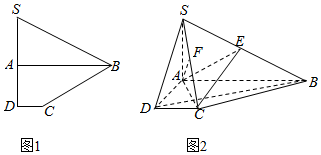 如图(1)所示,已知四边形SBCD是由直角△SAB和直角梯形ABCD拼接而成的,其中∠SAB=∠SDC=90°,且点A为线段SD的中点,AD=2DC=1,AB=SD,现将△SAB沿AB进行翻折,使得二面角S-AB-C的大小为90°,得到的图形如图(2)所示,连接SC,点E、F分别在线段SB、SC上.
如图(1)所示,已知四边形SBCD是由直角△SAB和直角梯形ABCD拼接而成的,其中∠SAB=∠SDC=90°,且点A为线段SD的中点,AD=2DC=1,AB=SD,现将△SAB沿AB进行翻折,使得二面角S-AB-C的大小为90°,得到的图形如图(2)所示,连接SC,点E、F分别在线段SB、SC上.