题目内容
设点M(x0,y0)在直线2x+y-2=0上运动,若在圆:x2+y2=1上存在点N,使得∠OMN=30°,则x0的取值范围是 .
考点:直线与圆相交的性质
专题:计算题,直线与圆
分析:根据圆的切线的性质,可知当过M点作圆的切线,切线与OM所成角是圆上的点与OM所成角的最大值,所以只需此角大于等于30°即可,此时半径,切线与OM构成直角三角形,因为切线与OM所成角大于等于30°所以OM小于等于半径的2倍,再用含x0的式子表示OM,即可求出x0的取值范围.
解答:
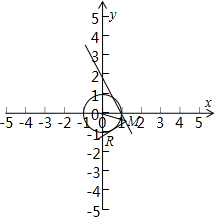 解:过M作⊙C切线交⊙C于R,
解:过M作⊙C切线交⊙C于R,
根据圆的切线性质,有∠OMR≥∠OMR=30°.
反过来,如果∠OMR≥30°,
则⊙C上存在一点N使得∠OMN=30°.
∴若圆C上存在点N,使∠OMN=30°,则∠OMR≥30°.
∵|OR|=1,
∴|OM|>2时不成立,
∴|OM|≤2.
又∵|OM|2=x02+y02=x02+(2-2x0)2=5x02-8x0+4
∴5x02-8x0+4≤4,
解得,0≤x0≤
.
∴x0的取值范围是[0,
]
故答案为:[0,
].
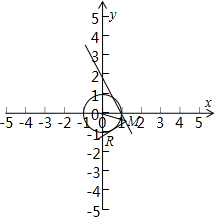 解:过M作⊙C切线交⊙C于R,
解:过M作⊙C切线交⊙C于R,根据圆的切线性质,有∠OMR≥∠OMR=30°.
反过来,如果∠OMR≥30°,
则⊙C上存在一点N使得∠OMN=30°.
∴若圆C上存在点N,使∠OMN=30°,则∠OMR≥30°.
∵|OR|=1,
∴|OM|>2时不成立,
∴|OM|≤2.
又∵|OM|2=x02+y02=x02+(2-2x0)2=5x02-8x0+4
∴5x02-8x0+4≤4,
解得,0≤x0≤
| 8 |
| 5 |
∴x0的取值范围是[0,
| 8 |
| 5 |
故答案为:[0,
| 8 |
| 5 |
点评:本题主要考查了直线与圆相切时切线的性质,以及一元二次不等式的解法,综合考察了学生的转化能力,计算能力,属于中档题.

练习册系列答案
相关题目
一几何体的三视图如图所示,则此几何体的体积是( )


A、32-
| ||
B、32-
| ||
| C、32-16π | ||
| D、32-32π |
下列函数中是偶函数的是( )
| A、y=x3 |
| B、y=cosx |
| C、y=2x |
| D、y=lnx |
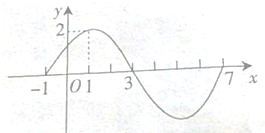 如图为函数y1=Asin(ωx+φ)的一段图象,已知A>0,ω>0,φ∈(-
如图为函数y1=Asin(ωx+φ)的一段图象,已知A>0,ω>0,φ∈(-