题目内容
私家车的尾气排放是造成雾霾天气的重要因素之一,因此在生活中我们应该提倡低碳生活,少开私家车,尽量选择绿色出行方式,为预防雾霾出一份力.为此,很多城市实施了机动车车尾号限行,我市某报社为了解市区公众对“车辆限行”的态度,随机抽查了50人,将调查情况进行整理后制成下表:
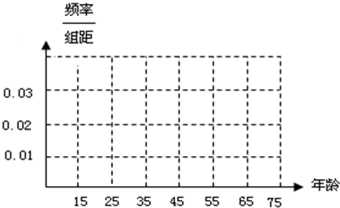
(Ⅰ)完成被调查人员的频率分布直方图;
(Ⅱ)若从年龄在[15,25),[25,35)的被调查者中各随机选取2人进行追踪调查,求恰有2人不赞成的概率;
(Ⅲ)在(Ⅱ)的条件下,再记选中的4人中不赞成“车辆限行”的人数为ξ,求随机变量ξ的分布列和数学期望.
| 年龄(岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75] |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 4 | 6 | 9 | 6 | 3 | 4 |

(Ⅰ)完成被调查人员的频率分布直方图;
(Ⅱ)若从年龄在[15,25),[25,35)的被调查者中各随机选取2人进行追踪调查,求恰有2人不赞成的概率;
(Ⅲ)在(Ⅱ)的条件下,再记选中的4人中不赞成“车辆限行”的人数为ξ,求随机变量ξ的分布列和数学期望.
考点:离散型随机变量的期望与方差,频率分布直方图,离散型随机变量及其分布列
专题:概率与统计
分析:(Ⅰ)由已知求出各组的频率和纵坐标,由此能作出被调查人员的频率分布直方图.
(Ⅱ)由表知年龄在[15,25)内的有5人,不赞成的有1人,年龄在[25,35)内的有10人,不赞成的有4人,由此利用互斥事件概率计算公式能求出恰有2人不赞成的概率.
(Ⅲ)ξ的所有可能取值为:0,1,2,3,分别求出相应的概率,由此能求出随机变量ξ的分布列和数学期望.
(Ⅱ)由表知年龄在[15,25)内的有5人,不赞成的有1人,年龄在[25,35)内的有10人,不赞成的有4人,由此利用互斥事件概率计算公式能求出恰有2人不赞成的概率.
(Ⅲ)ξ的所有可能取值为:0,1,2,3,分别求出相应的概率,由此能求出随机变量ξ的分布列和数学期望.
解答:
解:(Ⅰ)由已知得各组的频率分别是:
0.1,0.2,0.3,0.2,0.1,0.1,
∴图中各组的纵坐标分别是:
0.01,0.02,0.03,0.02,0.01,0.01,
由此能作出被调查人员的频率分布直方图,如右图:
(Ⅱ)由表知年龄在[15,25)内的有5人,
不赞成的有1人,
年龄在[25,35)内的有10人,不赞成的有4人,
∴恰有2人不赞成的概率为:
P(ξ=2)=
•
+
•
=
.…(7分)
(Ⅲ)ξ的所有可能取值为:0,1,2,3,…(6分)
P(ξ=0)=
•
=
,
P(ξ=1)=
•
+
•
=
,
P(ξ=3)=
•
=
,
所以ξ的分布列是:…(10分)
所以ξ的数学期望Eξ=
.…(12分)

0.1,0.2,0.3,0.2,0.1,0.1,
∴图中各组的纵坐标分别是:
0.01,0.02,0.03,0.02,0.01,0.01,
由此能作出被调查人员的频率分布直方图,如右图:
(Ⅱ)由表知年龄在[15,25)内的有5人,
不赞成的有1人,
年龄在[25,35)内的有10人,不赞成的有4人,
∴恰有2人不赞成的概率为:
P(ξ=2)=
| ||
|
| ||||
|
| ||
|
| ||
|
| 22 |
| 75 |
(Ⅲ)ξ的所有可能取值为:0,1,2,3,…(6分)
P(ξ=0)=
| ||
|
| ||
|
| 15 |
| 75 |
P(ξ=1)=
| ||
|
| ||
|
| ||
|
| ||||
|
| 34 |
| 75 |
P(ξ=3)=
| ||
|
| ||
|
| 4 |
| 75 |
所以ξ的分布列是:…(10分)
| ξ | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 6 |
| 5 |
点评:本题考查频率分布直方图的作法,考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意排列组合知识的合理运用.

练习册系列答案
相关题目
函数f(x)=lg(x-1)的定义域为( )
| A、(0,+∞) |
| B、(-∞,0) |
| C、(1,+∞) |
| D、(-∞,1) |
在△OAB中,|
|=a,|
|=b,OD是AB边上的高,若
=λ
,则实数λ等于( )
| OA |
| OB |
| AD |
| AB |
A、
| ||||||||||||
B、
| ||||||||||||
C、
| ||||||||||||
D、
|
若a<b<0,则下列不等式不成立是( )
A、
| ||||
B、
| ||||
| C、|a|>|b| | ||||
| D、a2>b2 |
已知等比数列{an},且a4+a8=
dx,则a6(a2+2a6+a10)的值为( )
| ∫ | 2 0 |
| 4-x2 |
| A、π2 | B、4 |
| C、π | D、-9π |
若圆(x-5)2+(y-1)2=r2上有且仅有两点到直线4x+3y+2=0的距离等于1,则r的取值范围为( )
| A、[4,6] |
| B、(4,6) |
| C、[5,7] |
| D、(5,7) |
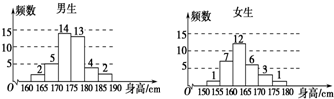 为了解学生身高情况,某校以10%的比例对高三年级的700名学生按性别进行分层抽样调查,测得身高情况的统计图如图:
为了解学生身高情况,某校以10%的比例对高三年级的700名学生按性别进行分层抽样调查,测得身高情况的统计图如图: