题目内容
设函数f(x)= 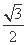 -
-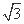 sin2ωx-sin ωxcos ωx(ω>0),且y=f(x)图象的一个对称中心到最近的对称轴的距离为
sin2ωx-sin ωxcos ωx(ω>0),且y=f(x)图象的一个对称中心到最近的对称轴的距离为 .
.
(1)求ω的值;
(2)求f(x)在区间[π, 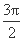 ]上的最大值和最小值.
]上的最大值和最小值.
解:(1)f(x)= 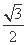 -
-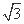 sin2ωx-sin ωxcos ωx
sin2ωx-sin ωxcos ωx
=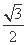 -
-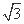 ·
· -
-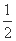 sin 2ωx
sin 2ωx
=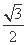 cos 2ωx-
cos 2ωx-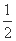 sin 2ωx
sin 2ωx
=-sin(2ωx- ).
).
因为图象的一个对称中心到最近的对称轴的距离为 ,
,
又ω>0,
所以 =4×
=4× ,
,
因此ω=1.
(2)由(1)知f(x)=-sin(2x- ).
).
当π≤x≤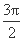 时,
时, ≤2x-
≤2x- ≤
≤ .
.
所以-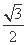 ≤sin(2x-
≤sin(2x- )≤1.
)≤1.
因此-1≤f(x)≤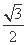 .
.
故f(x)在区间[π,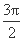 ]上的最大值和最小值分别为
]上的最大值和最小值分别为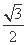 ,-1.
,-1.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目


 -
-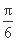 处取得最大值2,其图象与x轴的相邻两个交点的距离为
处取得最大值2,其图象与x轴的相邻两个交点的距离为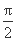 .
.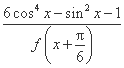 的值域.
的值域. 的值域为 .
的值域为 . 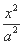 -
-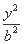 =1(a>0,b>0)的两个焦点,若F1、F2、P(0,2b)是正三角形的三个顶点,则双曲线的离心率为( )
=1(a>0,b>0)的两个焦点,若F1、F2、P(0,2b)是正三角形的三个顶点,则双曲线的离心率为( )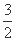 (B)2 (C)
(B)2 (C)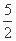 (D)3
(D)3 +
+ =1(a>b>0)上一点P向x轴作垂线,垂足恰为左焦点F1,A是椭圆与x轴正半轴的交点,B是椭圆与y轴正半轴的交点,且AB∥OP(O是坐标原点),则该椭圆的离心率是( )
=1(a>b>0)上一点P向x轴作垂线,垂足恰为左焦点F1,A是椭圆与x轴正半轴的交点,B是椭圆与y轴正半轴的交点,且AB∥OP(O是坐标原点),则该椭圆的离心率是( ) (B)
(B) (C)
(C)  (D)
(D)