题目内容
【题目】如图,直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() 是等腰三角形,
是等腰三角形,![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 上一点.
上一点.
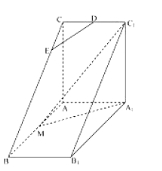
(I)若![]() 平面
平面![]() ,求
,求![]() ;
;
(II)平面![]() 将三棱柱
将三棱柱![]() 分成两个部分,求较小部分与较大部分的体积之比.
分成两个部分,求较小部分与较大部分的体积之比.
【答案】(I)![]() ;(II)
;(II)![]() .
.
【解析】
试题分析:(I)借助题设条件运用线面的位置关系求解;(II)借助题设运用体积割补的方法探求.
试题解析:
(I)取![]() 中点为
中点为![]() ,连接
,连接![]() ,
,![]() ,………………1分
,………………1分
∵![]() 分别
分别![]() ,
,![]() 为中点,
为中点,
∴![]() ,∴
,∴![]() 四点共面,………………3分
四点共面,………………3分
且平面![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,且
,且![]() 平面
平面![]() ,∴
,∴![]() .
.
∵![]() 为
为![]() 的中点,∴
的中点,∴![]() 是
是![]() 的中点,∴
的中点,∴![]() .………………6分
.………………6分
(II)因为三棱柱![]() 为直三棱柱,∴
为直三棱柱,∴![]() 平面
平面![]() ,
,
又![]() ,则
,则![]() 平面
平面![]() ,
,
设![]() ,又三角形
,又三角形![]() 是等腰三角形,所以
是等腰三角形,所以![]() .
.
如图,将几何体![]() 补成三棱柱
补成三棱柱![]() .
.
∴几何![]() 体的体积为:
体的体积为:
![]() .………………9分
.………………9分
又直三棱柱![]() 体积为:
体积为:![]() ,………………11分
,………………11分
故剩余的几何体棱台![]() 的体积为
的体积为![]() .
.
∴较小部分的体积与较大部分体积之比为:![]() .………………12分
.………………12分

【题目】设不等式组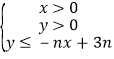 所表示的平面区域为
所表示的平面区域为![]() ,记
,记![]() 内的整点个数为
内的整点个数为![]() ,(整点即横、纵坐标均为整数的点)
,(整点即横、纵坐标均为整数的点)
(1)计算![]() 的值;
的值;
(2)求数列![]() 的通项公式
的通项公式![]() ;
;
(3)记数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,若对于一切的正整数
,若对于一切的正整数![]() ,总有
,总有![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【题目】菜农定期使用低害杀虫农药对蔬菜进行喷洒, 以防止害虫的危害, 但采集上市时蔬菜仍存有少量的残留农药, 食用时需要用清水清洗干净, 下表是用清水![]() (单位:千克) 清洗该蔬菜
(单位:千克) 清洗该蔬菜![]() 千克后, 蔬菜上残留的农药
千克后, 蔬菜上残留的农药![]() (单位:微克) 的统计表:
(单位:微克) 的统计表:
|
|
|
|
|
|
|
|
|
|
|
|
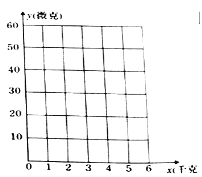
(1)在下面的坐标系中, 描出散点图, 并判断变量![]() 与
与![]() 的相关性;
的相关性;
(2)若用解析式![]() 作为蔬菜农药残量
作为蔬菜农药残量![]() 与用水量
与用水量![]() 的回归方程, 令
的回归方程, 令![]() ,计算平均值
,计算平均值![]() 与
与![]() ,完成以下表格(填在答题卡中) ,求出
,完成以下表格(填在答题卡中) ,求出![]() 与
与![]() 的回归方程.(
的回归方程.(![]() 精确到
精确到![]() )
)
|
|
|
|
|
|
|
|
|
|
|
|
| |||||
|
(3)对于某种残留在蔬菜上的农药,当它的残留量低于![]() 微克时对人体无害, 为了放心食用该蔬菜, 请
微克时对人体无害, 为了放心食用该蔬菜, 请
估计需要用多少千克的清水清洗一千克蔬菜?(精确到![]() ,参考数据
,参考数据![]() )
)
(附:线性回归方程![]() 中系数计算公式分别为;
中系数计算公式分别为;
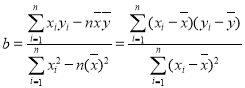 ,
, ![]() )
)
