Question

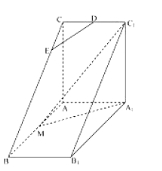
【题目】如图，在五棱锥中，平面,∥，∥，∥，, ，，是等腰三角形．

（1）求证：平面平面；

（2）求侧棱上是否存在点，使得与平面所成角大小为，若存在，求出点位置，若不存在，说明理由.

Answer 1

【答案】（1）详见解析（2）点为顶点时满足题意

【解析】

试题分析：（1）由边长可求得，结合可得到，从而可证明平面平面；（2）由设出动点Q坐标，结合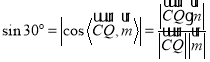求解值，从而确定点的位置

试题解析：（Ⅰ）证明：因为ABC=45°，AB=2，BC=4，所以在中，由余弦定理得：，解得，

所以，即，又PA⊥平面ABCDE，所以PA⊥，

又PA，所以，又AB∥CD，所以，又因为

，所以平面PCD⊥平面PAC

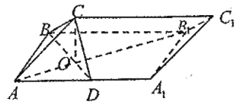
(2) 由（Ⅰ）知AB，AC，AP两两互相垂直，分别以AB，AC，AP为x，y，z轴建立如图所示的空间直角坐标系，由△PAB为等腰直角三角形，所以，

而，则

因为AC∥ED，CD⊥AC，所以四边形ACDE是直角梯形．

因为AE=2，∠ABC=45°，AE∥BC，所以∠BAE=135°，∠CAE=45°，

故，所以．

因此，设是平面PCD的一个法向量，则，解得x=0，y=z．取y=1，得，

假设

．

由解出，存在，点为顶点时满足题意