题目内容
20.设函数f(x)=ax3+3x,其图象在点(1,f(1))处的切线l与直线x-3y-7=0垂直,则直线l与y轴的交点坐标为( )| A. | (0,1) | B. | (0,2) | C. | (0,3) | D. | (0,4) |
分析 求出原函数的导函数,得到f′(1)=3a+3,由两直线垂直的条件可得3a+3=-3,求得a的值,代入原函数解析式,求出f(1),由直线方程的点斜式得到l的方程,求出直线l与y轴的交点坐标.
解答 解:由f(x)=ax3+3x,得f′(x)=3ax2+3,即有f′(1)=3a+3.
∵函数f(x)=ax3+3x在点(1,f(1))处的切线l与直线x-3y-7=0垂直,
∴3a+3=-3,解得a=-2.
∴f(x)=-2x3+3x,
则f(1)=-2+3=1.
∴切线方程为y-1=-3(x-1),
即6x+y-4=0.
取x=0,得y=4,
直线l与y轴的交点坐标为:(0,4).
故选:D.
点评 本题考查了利用导数研究函数在某点处的切线方程,在曲线上某点处的切线的斜率,就是函数在该点处的导数值,同时考查两直线垂直的条件,属于中档题.

练习册系列答案
相关题目
6.已知复数z=1+cosα+isinα(π<α<2π),则|$\overline{z}$|=( )
| A. | 2cos$\frac{α}{2}$ | B. | -2cos$\frac{α}{2}$ | C. | 2sin$\frac{α}{2}$ | D. | -2sin$\frac{α}{2}$ |
11.已知实数1,t,4成等比数列,则圆锥曲线$\frac{x^2}{t}+{y^2}$=1的离心率为( )
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$或$\sqrt{3}$ | C. | $\frac{1}{2}$或$\sqrt{3}$ | D. | $\frac{{\sqrt{2}}}{2}$或3 |
15.观察如图:

则第( )行的各数之和等于20112.

则第( )行的各数之和等于20112.
| A. | 2010 | B. | 2009 | C. | 1006 | D. | 1005 |
12.如图,根据样本的频率分布直方图,估计样本的中位数是( )


| A. | 10 | B. | 12 | C. | 13 | D. | 16 |
9.已知$sin(\frac{π}{4}+α)$=$\frac{1}{3}$,则sin2α的值为( )
| A. | $\frac{1}{3}$ | B. | $-\frac{1}{3}$ | C. | $-\frac{7}{9}$ | D. | $\frac{7}{9}$ |
10.已知F1,F2分别为双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右焦点,若点P是以F1F2为直径的圆与C右支的一个交点,PF1交C于另一点Q,且|PQ|=2|QF1|,则C的离心率为( )
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\frac{\sqrt{6}}{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
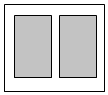 现需设计2016年春季湖北省重点高中联考协作体期中考试数学试卷,该试卷含有大小相等的左右相等两个矩形栏目(即图中阴影部分),这两栏的面积之和为720cm2,四周空白的宽度为4cm,两栏之间的中缝空白的宽度为2cm,设试卷的高和宽分别为xcm,ycm.
现需设计2016年春季湖北省重点高中联考协作体期中考试数学试卷,该试卷含有大小相等的左右相等两个矩形栏目(即图中阴影部分),这两栏的面积之和为720cm2,四周空白的宽度为4cm,两栏之间的中缝空白的宽度为2cm,设试卷的高和宽分别为xcm,ycm.