题目内容
已知函数f(x)=m·2x+t的图象经过点A(1,1),B(2,3)及C(n,Sn),Sn为数列{an}的前n项和.
(1)求an及Sn;
(2)若数列{cn}满足cn=6nan-n,求数列{cn}的前n项和Tn.
解析 (1)∵函数f(x)=m·2x+t的图象经过点A、B,
∴ ,∴
,∴ ,∴f(x)=2x-1,
,∴f(x)=2x-1,
∴Sn=2n-1,∴an=2n-1.
(2)cn=3n·2n-n,Tn=c1+c2+…+cn=3×(1×2+2×22+3×23+…+n·2n)-(1+2+…+n),
令Pn=1×2+2×22+…+n·2n ①
则2Pn=1×22+2×23+…+n·2n+1 ②
①-②得-Pn=2+22+…+2n-n·2n+1
= -n·2n+1=2n+1-2-n·2n+1,
-n·2n+1=2n+1-2-n·2n+1,
∴Pn=(n-1)2n+1+2,
∴Tn=3(n-1)2n+1+6- .
.

练习册系列答案
相关题目
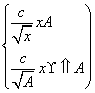 (A,c为常数).已知工人组装第4件产品用时30分钟,组装第A件产品用时15分钟,那么c和A的值分别是( ).
(A,c为常数).已知工人组装第4件产品用时30分钟,组装第A件产品用时15分钟,那么c和A的值分别是( ). 的图象是( )
的图象是( )

 ,b=log
,b=log ,c=log3
,c=log3 ,则a、b、c的大小关系是( )
,则a、b、c的大小关系是( ) 的图像与函数
的图像与函数 的图像恰有两个交点,则实数
的图像恰有两个交点,则实数 的取值范围是 .
的取值范围是 .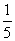 B.0 C.
B.0 C.