题目内容
已知向量a=(cos x,sin x),b=(-cos x,cos x),c=(-1,0).
(1)若x= ,求向量a与c的夹角;
,求向量a与c的夹角;
(2)当x∈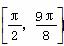 时,求函数f(x)=2a·b+1的最大值,并求此时x的值.
时,求函数f(x)=2a·b+1的最大值,并求此时x的值.
解析 (1) 
cos θ= =
=
=- .∵θ∈[0,π],∴θ=
.∵θ∈[0,π],∴θ= .
.
(2)f(x)=2a·b+1=2(-cos2x+sin xcos x)+1=2sin xcos x-(2cos2x-1)=sin 2x-cos 

练习册系列答案
相关题目
题目内容
已知向量a=(cos x,sin x),b=(-cos x,cos x),c=(-1,0).
(1)若x= ,求向量a与c的夹角;
,求向量a与c的夹角;
(2)当x∈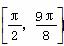 时,求函数f(x)=2a·b+1的最大值,并求此时x的值.
时,求函数f(x)=2a·b+1的最大值,并求此时x的值.
解析 (1) 
cos θ= =
=
=- .∵θ∈[0,π],∴θ=
.∵θ∈[0,π],∴θ= .
.
(2)f(x)=2a·b+1=2(-cos2x+sin xcos x)+1=2sin xcos x-(2cos2x-1)=sin 2x-cos 
