题目内容
设函数f(x)=|2x+1|-|x-3|
(1)求函数y=f(x)的最小值;
(2)若f(x)≥ax+
-
恒成立,求实数a的取值范围.
(1)求函数y=f(x)的最小值;
(2)若f(x)≥ax+
| a |
| 2 |
| 7 |
| 2 |
考点:分段函数的应用
专题:计算题,函数的性质及应用,不等式的解法及应用
分析:(1)去绝对值,分三段:x<-
,-
≤x≤3,x>3写出表达式,判断各段的单调性,得到最小值;
(2)令g(x)=ax+
-
,画出f(x)、g(x)的图象,通过直线绕点(-
,-
)旋转观察,即可得到a的取值范围.
| 1 |
| 2 |
| 1 |
| 2 |
(2)令g(x)=ax+
| a |
| 2 |
| 7 |
| 2 |
| 1 |
| 2 |
| 7 |
| 2 |
解答:
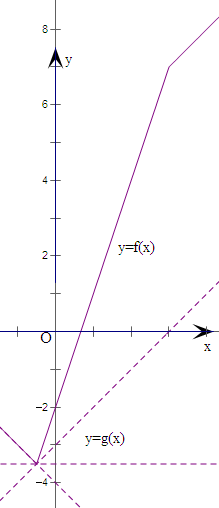 解:(1)由题意得f(x)=
解:(1)由题意得f(x)=
所以 f(x)在(-∞,-
)上单调递减,
在(-
,+∞)上单调递增.
所以当x=-
时y=f(x)取得最小值,
此时f(x)min=-
;
(2)由(1)及g(x)=ax+
-
,
可知y=g(x)恒过点过(-
,-
),
由图象可知-1≤a≤1.
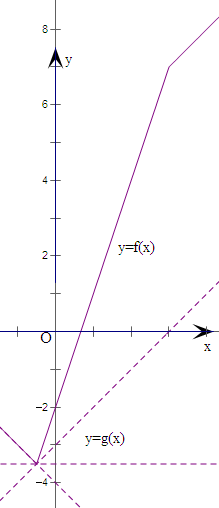 解:(1)由题意得f(x)=
解:(1)由题意得f(x)=
|
所以 f(x)在(-∞,-
| 1 |
| 2 |
在(-
| 1 |
| 2 |
所以当x=-
| 1 |
| 2 |
此时f(x)min=-
| 7 |
| 2 |
(2)由(1)及g(x)=ax+
| a |
| 2 |
| 7 |
| 2 |
可知y=g(x)恒过点过(-
| 1 |
| 2 |
| 7 |
| 2 |
由图象可知-1≤a≤1.
点评:本题考查绝对值函数的最值,注意写成分段函数的形式,讨论各段的单调性,从而求出最值,考查分段函数的图象和运用,不等式的恒成立问题转化为图象的位置关系,属于中档题.

练习册系列答案
相关题目