题目内容
棱台的上、下底面面积分别是2,4,高为3,则该棱台的体积是( )
A、18+6
| ||
B、6+2
| ||
| C、24 | ||
| D、18 |
考点:棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:直接利用棱台的体积公式,求出棱台的体积.
解答:
解:V=
(S+
+S′)h=
×(2+
+4)×3=6+2
故选:B.
| 1 |
| 3 |
| SS′ |
| 1 |
| 3 |
| 2×4 |
| 2 |
故选:B.
点评:本题考查棱台的体积,考查计算能力,是基础题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
下列函数在(-∞,0)上为增函数的是( )
| A、y=x3 | ||
| B、y=x2 | ||
| C、y=|x| | ||
D、y=(
|
已知f(x)=
,若f(x)为奇函数,则g(-1)的值为( )
|
| A、3 | B、-1 | C、-3 | D、1 |
不等式ax2+x+b>0的解集是(-2,3),则a+b的值是( )
| A、5 | B、-5 | C、10 | D、-10 |
已知函数f(x)满足f(x-1)=lgx,则不等式f(x)<0的解集为( )
| A、(-∞,1) |
| B、(1,2) |
| C、(-∞,0) |
| D、(-1,0) |
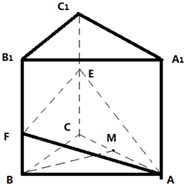 如图,直三棱柱ABC-A1B1C1中,底面是边长为2的正三角形,点E,F分别是
如图,直三棱柱ABC-A1B1C1中,底面是边长为2的正三角形,点E,F分别是